搜索到
15
篇与
的结果
-
 从0开始自制解释器——重构代码 在上一篇文章中,完成了对括号的支持,这样整个程序就可以解析普通的算术表达式了。但是在解析两个括号的过程中发现有大量的地方需要进行索引的回退操作,索引的操作应该保证能得到争取的token,这个步骤应该放在词法分析的阶段,如果在语法分析阶段还要考虑下层词法分析的过程,就显得有些复杂了。而且随着后续支持的符号越来越多,可能又得在大量的地方进行这种索引变更的操作,代码将难以理解和维护。因此这里先停下来进行一次代码的重构。基本架构这里的代码我按照教程里面的结构进行组织。将按照程序的逻辑分为3层,最底层负责操作字符串的索引保证下次获取token的时候索引能在正确的位置。第二层是词法分析部分,负责给字符串的每个部分都打上对应的token。第三个部分是语法分析的部分,它负责解析之前设计的BNF范式,并计算对应的结果。详细的代码上面给出模块划分的概要可能没怎么说清楚,下面将通过代码来进行详细的说明。Token 模块为了支持这个设计,首先变更一下全局变量的定义,现在定义的全局变量如下所示extern Token g_currentToken; //当前token extern int g_nPosition; //当前字符索引的位置 extern char g_currentChar; //当前字符串之前通过 get_next_char() 来返回当前指向的token并变更索引的时候发现我们在任何时候想获取当前指向的字符时永远要变更索引,这样就不得不考虑在某些时候要进行索引的回退。比如在解析整数退出的时候,此时当前字符已经指向下一个字符了,但是我们在接下来解析其他符号的时候调用 get_next_char() 导致索引多增加了一个。这种情况经常出现,因此这里使用全局变量保存当前字符,只在需要进行索引增加的时候进行增加。另外我们不希望上层来直接操作这个索引,因此在最底层的Token模块提供一个名为 advance() 的函数用于将索引加一,并获取之后的字符。它的定义如下void advance() { g_nPosition++; // 如果到达字符串尾部,索引不再增加 if (g_nPosition >= strlen(g_pszUserBuf)) { g_currentChar = '\0'; } else { g_currentChar = g_pszUserBuf[g_nPosition]; } }这样在对应需要用到当前字符的位置就不再使用 get_next_char() , 而是改用全局变量 g_currentChar。例如现在的 skip_whitespace 函数现在的定义如下void skip_whitespace() { while (is_space(g_currentChar)) { advance(); } }这样我们在获取下一个token的时候只在必要的时候进行索引的递增。lex 模块由于打标签的工作交个底层的Token模块了,该模块主要用来实现词法分析的功能,也就是给各个部分打上标签,根据之前Token部分提供的接口,需要对 get_next_token 函数进行修改。bool get_next_token() { dyncstring_reset(&g_currentToken.value); while (g_currentChar != '\0') { if (is_digit(g_currentChar)) { g_currentToken.type = CINT; parser_number(&g_currentToken.value); return true; } else if (is_space(g_currentChar)) { skip_whitespace(); } else { switch (g_currentChar) { case '+': g_currentToken.type = PLUS; dyncstring_catch(&g_currentToken.value, '+'); advance(); break; case '-': g_currentToken.type = MINUS; dyncstring_catch(&g_currentToken.value, '-'); advance(); break; case '*': g_currentToken.type = DIV; dyncstring_catch(&g_currentToken.value, '*'); advance(); break; case '/': g_currentToken.type = MUL; dyncstring_catch(&g_currentToken.value, '/'); advance(); break; case '(': g_currentToken.type = LPAREN; dyncstring_catch(&g_currentToken.value, '('); advance(); break; case ')': g_currentToken.type = RPAREN; dyncstring_catch(&g_currentToken.value, ')'); advance(); break; case '\0': g_currentToken.type = END_OF_FILE; break; default: return false; } return true; } } return true; }在这个函数中,将不再通过输出参数来返回当前的token,而是直接修改全局变量。同时也不再使用get_next_char 函数来获取当前指向的字符,而是直接使用全局变量。并且在适当的时机调用advance 来实现递增。另外在上层我们直接使用 g_currentToken 拿到当前的token,而在适当的时机调用新增的eat() 函数来实现更新token的操作。bool eat(LPTOKEN pToken, ETokenType eType) { if (pToken->type == eType) { get_next_token(); return true; } return false; }该函数接受两个参数,第一个是当前token的值,第二个是我们期望当前token是何种类型。如果当前token的类型与期望的不符则报错,否则更新token。interpreter 模块该模块主要负责解析根据前面的BNF范式来完成计算并解析内容。这个模块提供三个函数get_factor、get_term、expr。这三个函数的功能没有变化,只是在实现上依靠lex 模块提供的功能。主要思路是直接使用 g_currentToken 这个全局变量来获得当前的token,使用 eat() 来更新并获得下一个token的值。这里我们以get_factor() 函数为例int get_factor(bool* pRet) { int value = 0; if (g_currentToken.type == CINT) { value = atoi(g_currentToken.value.pszBuf); *pRet = eat(&g_currentToken, CINT); } else { if (g_currentToken.type == LPAREN) { bool bValid = true; bValid = eat(&g_currentToken, LPAREN); value = expr(&bValid); bValid = eat(&g_currentToken, RPAREN); *pRet = bValid; } } return value; }与前面分析的相同,该函数主要负责获取整数和计算括号中子表达式的值。在解析完整数和括号中的子表达式之后,需要调用eat分别跳过对应的值。只是在识别到括号之后需要跳过左右两个括号。这样就完成了对应的分层,每层只负责自己该做的事。不用在上层考虑修改索引的问题,结构也更加清晰,未来在添加功能的时候也更加方便。剩下几个函数就不再贴出代码了,感兴趣的小伙伴可以去对应的GitHub仓库上查阅相关代码。
从0开始自制解释器——重构代码 在上一篇文章中,完成了对括号的支持,这样整个程序就可以解析普通的算术表达式了。但是在解析两个括号的过程中发现有大量的地方需要进行索引的回退操作,索引的操作应该保证能得到争取的token,这个步骤应该放在词法分析的阶段,如果在语法分析阶段还要考虑下层词法分析的过程,就显得有些复杂了。而且随着后续支持的符号越来越多,可能又得在大量的地方进行这种索引变更的操作,代码将难以理解和维护。因此这里先停下来进行一次代码的重构。基本架构这里的代码我按照教程里面的结构进行组织。将按照程序的逻辑分为3层,最底层负责操作字符串的索引保证下次获取token的时候索引能在正确的位置。第二层是词法分析部分,负责给字符串的每个部分都打上对应的token。第三个部分是语法分析的部分,它负责解析之前设计的BNF范式,并计算对应的结果。详细的代码上面给出模块划分的概要可能没怎么说清楚,下面将通过代码来进行详细的说明。Token 模块为了支持这个设计,首先变更一下全局变量的定义,现在定义的全局变量如下所示extern Token g_currentToken; //当前token extern int g_nPosition; //当前字符索引的位置 extern char g_currentChar; //当前字符串之前通过 get_next_char() 来返回当前指向的token并变更索引的时候发现我们在任何时候想获取当前指向的字符时永远要变更索引,这样就不得不考虑在某些时候要进行索引的回退。比如在解析整数退出的时候,此时当前字符已经指向下一个字符了,但是我们在接下来解析其他符号的时候调用 get_next_char() 导致索引多增加了一个。这种情况经常出现,因此这里使用全局变量保存当前字符,只在需要进行索引增加的时候进行增加。另外我们不希望上层来直接操作这个索引,因此在最底层的Token模块提供一个名为 advance() 的函数用于将索引加一,并获取之后的字符。它的定义如下void advance() { g_nPosition++; // 如果到达字符串尾部,索引不再增加 if (g_nPosition >= strlen(g_pszUserBuf)) { g_currentChar = '\0'; } else { g_currentChar = g_pszUserBuf[g_nPosition]; } }这样在对应需要用到当前字符的位置就不再使用 get_next_char() , 而是改用全局变量 g_currentChar。例如现在的 skip_whitespace 函数现在的定义如下void skip_whitespace() { while (is_space(g_currentChar)) { advance(); } }这样我们在获取下一个token的时候只在必要的时候进行索引的递增。lex 模块由于打标签的工作交个底层的Token模块了,该模块主要用来实现词法分析的功能,也就是给各个部分打上标签,根据之前Token部分提供的接口,需要对 get_next_token 函数进行修改。bool get_next_token() { dyncstring_reset(&g_currentToken.value); while (g_currentChar != '\0') { if (is_digit(g_currentChar)) { g_currentToken.type = CINT; parser_number(&g_currentToken.value); return true; } else if (is_space(g_currentChar)) { skip_whitespace(); } else { switch (g_currentChar) { case '+': g_currentToken.type = PLUS; dyncstring_catch(&g_currentToken.value, '+'); advance(); break; case '-': g_currentToken.type = MINUS; dyncstring_catch(&g_currentToken.value, '-'); advance(); break; case '*': g_currentToken.type = DIV; dyncstring_catch(&g_currentToken.value, '*'); advance(); break; case '/': g_currentToken.type = MUL; dyncstring_catch(&g_currentToken.value, '/'); advance(); break; case '(': g_currentToken.type = LPAREN; dyncstring_catch(&g_currentToken.value, '('); advance(); break; case ')': g_currentToken.type = RPAREN; dyncstring_catch(&g_currentToken.value, ')'); advance(); break; case '\0': g_currentToken.type = END_OF_FILE; break; default: return false; } return true; } } return true; }在这个函数中,将不再通过输出参数来返回当前的token,而是直接修改全局变量。同时也不再使用get_next_char 函数来获取当前指向的字符,而是直接使用全局变量。并且在适当的时机调用advance 来实现递增。另外在上层我们直接使用 g_currentToken 拿到当前的token,而在适当的时机调用新增的eat() 函数来实现更新token的操作。bool eat(LPTOKEN pToken, ETokenType eType) { if (pToken->type == eType) { get_next_token(); return true; } return false; }该函数接受两个参数,第一个是当前token的值,第二个是我们期望当前token是何种类型。如果当前token的类型与期望的不符则报错,否则更新token。interpreter 模块该模块主要负责解析根据前面的BNF范式来完成计算并解析内容。这个模块提供三个函数get_factor、get_term、expr。这三个函数的功能没有变化,只是在实现上依靠lex 模块提供的功能。主要思路是直接使用 g_currentToken 这个全局变量来获得当前的token,使用 eat() 来更新并获得下一个token的值。这里我们以get_factor() 函数为例int get_factor(bool* pRet) { int value = 0; if (g_currentToken.type == CINT) { value = atoi(g_currentToken.value.pszBuf); *pRet = eat(&g_currentToken, CINT); } else { if (g_currentToken.type == LPAREN) { bool bValid = true; bValid = eat(&g_currentToken, LPAREN); value = expr(&bValid); bValid = eat(&g_currentToken, RPAREN); *pRet = bValid; } } return value; }与前面分析的相同,该函数主要负责获取整数和计算括号中子表达式的值。在解析完整数和括号中的子表达式之后,需要调用eat分别跳过对应的值。只是在识别到括号之后需要跳过左右两个括号。这样就完成了对应的分层,每层只负责自己该做的事。不用在上层考虑修改索引的问题,结构也更加清晰,未来在添加功能的时候也更加方便。剩下几个函数就不再贴出代码了,感兴趣的小伙伴可以去对应的GitHub仓库上查阅相关代码。 -
 从0开始自制解释器——添加对括号的支持 在上一篇我们添加了对乘除法的支持,也介绍了BNF范式,并且针对当前的算术表达式写出了对应的范式,同时根据范式给出相应的代码实现。这篇我们将继续为算数表达式添加对括号的支持。对应的BNF 范式在上一篇我们给出了乘除法对应的范式<expr>::=<term>{(PLUS|MINUS)<term>} <term>::=<factor>{(DIV|MUL)<factor>} <factor>::={(0|1|2|3|4|5|6|7|8|9)}针对乘除法的优先级比加减法高,我们的做法是将乘除法单独作为一个部分,然后在最外层表达式中只处理加减法。基于这种思路,我们来看如何处理括号的问题。例如下面的算数表达式((1+2)*3+4) - (5 - 6 / 3)这里我们直接给出对应的文法,然后再来分析一下该如何由这个文法得到对应的表达式<expr>::=<term>{(PLUS|MINUS)<term>} <term>::=<factor>{(DIV|MUL)<factor>} <factor>::=({(0|1|2|3|4|5|6|7|8|9|)})|LPAREN<expr>RPAREN首先根据表达式,它应该由两个term来组成 expr = term - term接着看看两个term,它们并不是单纯的加法运算,所以两个term应该只有单纯的一个factor,也就是 expr = factor - factor因为最外层都有括号,所以再次展开 expr = (expr1) - (expr2)这时就又到了分析expr的过程了,左侧的expr最外层是一个加法,所以这里可以得到 expr1 = term + term右侧的expr 最外层是一个减法,也就是 expr2 = term - term结合最外层的表达式可以得到 expr = (term1 + term2) - (term3 - term4)term1 部分有一个乘法,所以它可以解析为 term1 = factor * factorterm2 部分就是单独的数字所以可以得到 term2 = factor,并且进一步得到 term2=4term3 部分就是单纯的数字,可以得到 term3 = factor,并且进一步得到 term3=5term4 部分有一个除法,所以它可以解析为 term3 = factor / factor此时整个表达式可以表示为 expr = (factor1 * factor2 + 4) - (5 - factor3 / factor4)factor1 本身也是一个括号,加表达式,所以它可以表示为 factor1 = (expr)factor2 是一个数字,所以它表示为 factor2 = 3factor3 是一个数字,所以它表示为 factor3 = 6factor4 是一个数字,所以它表示为 factor4 = 3此时表达式可以是 expr = ((expr1) * 3 + 4) - (5 - 6 / 3)此时再次分析这个 expr1 可以得到 expr1 = 1+2这个时候,整个表达式就出来了 expr = ((1+2) * 3 + 4) - (5 - 6 / 3)用图来表示大概可以表示如下代码实现有了范式,我们就可以按照范式来组织代码实现。首先我们先在 ETokenType 中添加针对括号的标签typedef enum e_TokenType { CINT = 0, //整数 PLUS, //加法 MINUS, //减法 DIV, //乘法 MUL, //除法 LPAREN, //左括号 RPAREN, //右括号 END_OF_FILE // 字符串末尾结束符号 }ETokenType;然后在 get_next_token 函数中添加对括号进行词法分析并打标签的功能bool get_next_token(LPTOKEN pToken) { char c = get_next_char(); dyncstring_reset(&pToken->value); if (is_digit(c)) { dyncstring_catch(&pToken->value, c); pToken->type = CINT; parser_number(&pToken->value); } else if(is_space(c)) { skip_whitespace(); return get_next_token(pToken); } else { switch (c) { case '+': pToken->type = PLUS; break; case '-': pToken->type = MINUS; break; case '*': pToken->type = DIV; break; case '/': pToken->type = MUL; break; case '(': pToken->type = LPAREN; break; case ')': pToken->type = RPAREN; break; case '\0': pToken->type = END_OF_FILE; break; default: return false; } } return true; }这里我对这个函数进行了一些改写,针对依靠单个字符就能打上标签的采用switc来进行处理,像空白字符、数字这种有多种字符类型的就采用普通的if处理。然后在get_oper 中添加对括号的识别 if (get_next_token(&token) && (token.type == PLUS || token.type == MINUS || token.type == DIV || token.type == MUL || token.type == LPAREN || token.type == RPAREN)) { oper = token.type; if (pRet) *pRet = true; }然后根据文法,get_factor 需要能够返回一个 expr的结果,所以这里需要添加以下代码 if (token.type == LPAREN) { bool bValid = true; value = expr(&bValid); if (!bValid) *pRet = false; if (get_next_token(&token) && token.type == RPAREN) *pRet = true; else *pRet = false; }如果我们得到的标签不为括号则按照原来的处理方式来处理,如果是括号,则将括号中的内容作为表达式并计算表达式的值,作为整数来返回。之前的expr 函数我们仅仅将结果打印并返回是否解析成功,这里需要做一些改进。我们使用一个传出参数来返回解析是否成功,而将计算结果作为值进行返回。另外需要特别注意的是,我们将反括号的判断放到了 get_factor 函数中,所以在 get_term 和 expr 中,遇到反括号应该考虑对位置索引进行递减,并且遇到反括号应该认为到达末尾并推出。这里的代码就不贴出来了。有兴趣的小伙伴可以看github上上传的代码。地址
从0开始自制解释器——添加对括号的支持 在上一篇我们添加了对乘除法的支持,也介绍了BNF范式,并且针对当前的算术表达式写出了对应的范式,同时根据范式给出相应的代码实现。这篇我们将继续为算数表达式添加对括号的支持。对应的BNF 范式在上一篇我们给出了乘除法对应的范式<expr>::=<term>{(PLUS|MINUS)<term>} <term>::=<factor>{(DIV|MUL)<factor>} <factor>::={(0|1|2|3|4|5|6|7|8|9)}针对乘除法的优先级比加减法高,我们的做法是将乘除法单独作为一个部分,然后在最外层表达式中只处理加减法。基于这种思路,我们来看如何处理括号的问题。例如下面的算数表达式((1+2)*3+4) - (5 - 6 / 3)这里我们直接给出对应的文法,然后再来分析一下该如何由这个文法得到对应的表达式<expr>::=<term>{(PLUS|MINUS)<term>} <term>::=<factor>{(DIV|MUL)<factor>} <factor>::=({(0|1|2|3|4|5|6|7|8|9|)})|LPAREN<expr>RPAREN首先根据表达式,它应该由两个term来组成 expr = term - term接着看看两个term,它们并不是单纯的加法运算,所以两个term应该只有单纯的一个factor,也就是 expr = factor - factor因为最外层都有括号,所以再次展开 expr = (expr1) - (expr2)这时就又到了分析expr的过程了,左侧的expr最外层是一个加法,所以这里可以得到 expr1 = term + term右侧的expr 最外层是一个减法,也就是 expr2 = term - term结合最外层的表达式可以得到 expr = (term1 + term2) - (term3 - term4)term1 部分有一个乘法,所以它可以解析为 term1 = factor * factorterm2 部分就是单独的数字所以可以得到 term2 = factor,并且进一步得到 term2=4term3 部分就是单纯的数字,可以得到 term3 = factor,并且进一步得到 term3=5term4 部分有一个除法,所以它可以解析为 term3 = factor / factor此时整个表达式可以表示为 expr = (factor1 * factor2 + 4) - (5 - factor3 / factor4)factor1 本身也是一个括号,加表达式,所以它可以表示为 factor1 = (expr)factor2 是一个数字,所以它表示为 factor2 = 3factor3 是一个数字,所以它表示为 factor3 = 6factor4 是一个数字,所以它表示为 factor4 = 3此时表达式可以是 expr = ((expr1) * 3 + 4) - (5 - 6 / 3)此时再次分析这个 expr1 可以得到 expr1 = 1+2这个时候,整个表达式就出来了 expr = ((1+2) * 3 + 4) - (5 - 6 / 3)用图来表示大概可以表示如下代码实现有了范式,我们就可以按照范式来组织代码实现。首先我们先在 ETokenType 中添加针对括号的标签typedef enum e_TokenType { CINT = 0, //整数 PLUS, //加法 MINUS, //减法 DIV, //乘法 MUL, //除法 LPAREN, //左括号 RPAREN, //右括号 END_OF_FILE // 字符串末尾结束符号 }ETokenType;然后在 get_next_token 函数中添加对括号进行词法分析并打标签的功能bool get_next_token(LPTOKEN pToken) { char c = get_next_char(); dyncstring_reset(&pToken->value); if (is_digit(c)) { dyncstring_catch(&pToken->value, c); pToken->type = CINT; parser_number(&pToken->value); } else if(is_space(c)) { skip_whitespace(); return get_next_token(pToken); } else { switch (c) { case '+': pToken->type = PLUS; break; case '-': pToken->type = MINUS; break; case '*': pToken->type = DIV; break; case '/': pToken->type = MUL; break; case '(': pToken->type = LPAREN; break; case ')': pToken->type = RPAREN; break; case '\0': pToken->type = END_OF_FILE; break; default: return false; } } return true; }这里我对这个函数进行了一些改写,针对依靠单个字符就能打上标签的采用switc来进行处理,像空白字符、数字这种有多种字符类型的就采用普通的if处理。然后在get_oper 中添加对括号的识别 if (get_next_token(&token) && (token.type == PLUS || token.type == MINUS || token.type == DIV || token.type == MUL || token.type == LPAREN || token.type == RPAREN)) { oper = token.type; if (pRet) *pRet = true; }然后根据文法,get_factor 需要能够返回一个 expr的结果,所以这里需要添加以下代码 if (token.type == LPAREN) { bool bValid = true; value = expr(&bValid); if (!bValid) *pRet = false; if (get_next_token(&token) && token.type == RPAREN) *pRet = true; else *pRet = false; }如果我们得到的标签不为括号则按照原来的处理方式来处理,如果是括号,则将括号中的内容作为表达式并计算表达式的值,作为整数来返回。之前的expr 函数我们仅仅将结果打印并返回是否解析成功,这里需要做一些改进。我们使用一个传出参数来返回解析是否成功,而将计算结果作为值进行返回。另外需要特别注意的是,我们将反括号的判断放到了 get_factor 函数中,所以在 get_term 和 expr 中,遇到反括号应该考虑对位置索引进行递减,并且遇到反括号应该认为到达末尾并推出。这里的代码就不贴出来了。有兴趣的小伙伴可以看github上上传的代码。地址 -
 从0开始自制解释器——添加对乘除法的支持 在上一篇中,我们实现了对减法的支持,并且介绍了语法图。针对简单的语法进行描述,用语法图描述当然是没问题的。但是针对一些复杂的语法进行描述,如果每个部分都通过语法图来描述就显得有些繁琐了。这篇我们先介绍另一种描述语法的方式,并进一步介绍一些关于语法分析的知识。BNF范式与上下文无关文法巴科斯范式 以美国人巴科斯(Backus)和丹麦人诺尔(Naur)的名字命名的一种形式化的语法表示方法,用来描述语法的一种形式体系,是一种典型的元语言。又称巴科斯-诺尔形式(Backus-Naur form)。它不仅能严格地表示语法规则,而且所描述的语法是与上下文无关的。它以递归方式描述语言中的各种成分,凡遵守其规则的程序就可保证语法上的正确性。它具有语法简单,表示明确,便于语法分析和编译的特点。BNF表示语法规则的方式为:非终结符用尖括号括起。每条规则的左部是一个非终结符,右部是由非终结符和终结符组成的一个符号串,中间一般以“::=”分开。具有相同左部的规则可以共用一个左部,各右部之间以直竖“|”隔开。所谓非终结符就是语言中某些抽象的概念不能直接出现在语言中的符号,终结符就是可以直接出现在语言中的符号。其实这些都是一些官话,初看起来只觉得拗口和难以理解,但是它的形式非常简单。它主要是用下面几个符号来表达含义使用<>来表示必须包含的部分使用[]来表示可选部分使用{}来表示可以重复0次或者无数次使用|来表示左右两边任选一部分,相当于OR使用::=来表示被定义为现在来给出具体的例子,我们都看过《西游记》,里面的取经4人组包括唐僧、孙悟空、猪八戒和沙僧。使用BNF范式进行定义,可以写成 <取经团队>::=<唐僧><孙悟空><猪八戒><沙僧>。我们再来举一个例子,我们知道一个文章由若干个段落组成、一个段落由若干个句子组成、一个句子由符合一定语法规则的汉字组成并且以句号作为结尾。我们简单的将句子的语法规则定义为主谓宾三个部分。而这里的主谓宾我们简单的用一些名词和动词来定义。因此这里的一系列结构可以定义为如下内容<文章>::={<段落>}<段落>::={<句子>}<句子>::=<主语><谓语><宾语>。<主语>::=人|狗|猫|天<谓语>::=吃|抓|下<宾语>::=饭|雨|肉|鱼根据这个表达式我们很容易的推出类似 人吃饭。、天下雨。、猫抓鱼。 这样的句子。相信到这里小伙伴应该明白BNF范式的一些基本概念和使用方式了。我们再来插入一个题外话,既然这里提到BNF范式是一种上下文无关文法,那什么是上下文、什么是上下文无关。先别着急了解概念,我们仍然通过例子来说明。在上述的句子的定义中,我们一共可以生成 4 * 3 * 4 = 48 种 结果,我们可以获得类似 人吃饭。、猫抓鱼。这种有意义的句子,也可能产生像天吃鱼。、人下雨 这种读起来感觉别扭的非正常语句。但是在上下文无关的语法中,主语宾语和谓语的内容没有相互关联,也就是说谓语和宾语的产生与主语无关。那上下文有关的文法呢?这里为了产生一些有意义的句子,我们给它加上一些限定。例如人后面只能接 吃 抓作为谓语、而当吃作为谓语时只能将 饭、肉、鱼作为宾语。针对这种需求,我们可以进行如下定义<句子>::=<主语><谓语><宾语>。<主语>::=人|狗|猫|天人<谓语>::=人(吃|抓)吃<宾语>::=吃(饭|肉|鱼)这样我们对这个产生式进行了一些限定,当主语是人的时候,谓语只能产生吃和抓这样的宾语。这种情况下的描述就被称之为上下文有关。上下文无关我自己的理解就是后续表达式的产生不依赖前面已产生的内容。而上下文有关的含义则与之相法。这个上下文就跟我们这么多年阅读理解题里面写的“请根据上下文来理解某个词表达了作者怎样的心情”这里的上下文类似。当然更加规范的说法就是,在应用一个产生式进行推导时,前后已经推导出的部分结果就是上下文。上下文无关就是只要文法的定义里面有一个定义,不管前面的产生串是什么都可以应用相应的产生推导后面的内容。代码编写上面的定义只是开胃菜,希望通过上面的描述,小伙伴能够理解BNF范式的应用,至于上下文无关和上下文有关。这些暂时不用考虑,毕竟我们目前还是在做上下文无关文法相关的内容。这里我们要支持乘法和除法,首先要做的就是在 ETokenType 结构中添加对乘法和除法相关的定义typedef enum e_TokenType { CINT = 0, //整数 PLUS, //加法 MINUS, //减法 DIV, //乘法 MUL, //除法 END_OF_FILE // 字符串末尾结束符号 }ETokenType;接着在 get_next_token和 get_oper() 函数中添加对这两个运算符的支持// get_next_token else if (c == '*') { pToken->type = DIV; dyncstring_catch(&pToken->value, '*'); } else if (c == '/') { pToken->type = MUL; dyncstring_catch(&pToken->value, '/'); } // get_oper if (get_next_token(&token) && (token.type == PLUS || token.type == MINUS || token.type == DIV || token.type == MUL)) { oper = token.type; if (pRet) *pRet = true; }现在词法分析部分已经可以支持乘除法的符号解析了。接着来完成语法分析的部分。首先我们来定义一下这个简单计算器的文法。<expr>::=<term>{<oper><term>} <term>::={0|1|2|3|4|5|6|7|8|9} <oper>::=PLUS|MINUS|DIV|MUL回忆一下上一节给出的语法图,理解这个表达式并不算困难。但是这里我们定义的文法有一个问题,就是从文法上体现不出运算的优先级。学过小学数学的都知道算数运算中优先计算乘除法,最后算加减法。但是根据这个文法我们无法体现出乘除法的优先级。因此这里我们需要修改定义。优先计算乘除法在文法上可以理解成,乘除法单独成一个部分,我们获取这个部分的计算结果最后与其他部分一起计算加减法。用BNF范式来体现就是<expr>::=<term>{(PLUS|MINUS)<term>} <term>::=<factor>{(DIV|MUL)<factor>} <factor>::={0|1|2|3|4|5|6|7|8|9}与语法图类似,范式也可以很容易转化为代码。允许出现多次的我们在代码实现上体现为循环。而文法中相关的定义我们直接采用一些get方式来获取对应被打上标记的值即可。上述文法描述可以转化为如下的c 代码int expr() { bool bRet = false; int result = get_term(&bRet); int bEOF = false; do { ETokenType oper = get_oper(&bRet); switch (oper) { case PLUS: { int num = get_term(&bRet); if(bRet) result += num; } break; case MINUS: { int num = get_term(&bRet); if(bRet) result -= num; } break; case END_OF_FILE: printf("%d\n", result); bEOF = true; break; default: bRet = false; break; } } while (bRet && !bEOF); if (!bRet) { printf("Syntax Error!\n"); } return 0; }上述expr的定义就是由一个term加若干个 +|- 和后面的若干个term 来组成,因此这里有一个循环。来取出所有term 和所有加减法,并进行计算。int get_term(bool* pValid) { int result = get_factor(pValid); int bEOF = false; do { ETokenType oper = get_oper(pValid); switch (oper) { case DIV: { int num = get_factor(pValid); if (*pValid) result *= num; } break; case MUL: { int num = get_factor(pValid); if (*pValid) result /= num; } break; case PLUS: case MINUS: { g_pPosition--; bEOF = true; } break; case END_OF_FILE: { g_pPosition--; bEOF = true; } } } while (pValid && !bEOF); return result; }而term 则是由整数以及若干个乘除法和另一个整数组成,所以代码中也用循环来取一直到取到不是这个term 定义所组成的部。注意这里与之前一样,当取到term的结束部分,我们仍然需要将索引进行递减。而最终的oper 和 factor 则保持原来的算法不变。好了,本篇到此也就结束了,小伙伴可以到该位置 取出代码来进行阅读和修改。
从0开始自制解释器——添加对乘除法的支持 在上一篇中,我们实现了对减法的支持,并且介绍了语法图。针对简单的语法进行描述,用语法图描述当然是没问题的。但是针对一些复杂的语法进行描述,如果每个部分都通过语法图来描述就显得有些繁琐了。这篇我们先介绍另一种描述语法的方式,并进一步介绍一些关于语法分析的知识。BNF范式与上下文无关文法巴科斯范式 以美国人巴科斯(Backus)和丹麦人诺尔(Naur)的名字命名的一种形式化的语法表示方法,用来描述语法的一种形式体系,是一种典型的元语言。又称巴科斯-诺尔形式(Backus-Naur form)。它不仅能严格地表示语法规则,而且所描述的语法是与上下文无关的。它以递归方式描述语言中的各种成分,凡遵守其规则的程序就可保证语法上的正确性。它具有语法简单,表示明确,便于语法分析和编译的特点。BNF表示语法规则的方式为:非终结符用尖括号括起。每条规则的左部是一个非终结符,右部是由非终结符和终结符组成的一个符号串,中间一般以“::=”分开。具有相同左部的规则可以共用一个左部,各右部之间以直竖“|”隔开。所谓非终结符就是语言中某些抽象的概念不能直接出现在语言中的符号,终结符就是可以直接出现在语言中的符号。其实这些都是一些官话,初看起来只觉得拗口和难以理解,但是它的形式非常简单。它主要是用下面几个符号来表达含义使用<>来表示必须包含的部分使用[]来表示可选部分使用{}来表示可以重复0次或者无数次使用|来表示左右两边任选一部分,相当于OR使用::=来表示被定义为现在来给出具体的例子,我们都看过《西游记》,里面的取经4人组包括唐僧、孙悟空、猪八戒和沙僧。使用BNF范式进行定义,可以写成 <取经团队>::=<唐僧><孙悟空><猪八戒><沙僧>。我们再来举一个例子,我们知道一个文章由若干个段落组成、一个段落由若干个句子组成、一个句子由符合一定语法规则的汉字组成并且以句号作为结尾。我们简单的将句子的语法规则定义为主谓宾三个部分。而这里的主谓宾我们简单的用一些名词和动词来定义。因此这里的一系列结构可以定义为如下内容<文章>::={<段落>}<段落>::={<句子>}<句子>::=<主语><谓语><宾语>。<主语>::=人|狗|猫|天<谓语>::=吃|抓|下<宾语>::=饭|雨|肉|鱼根据这个表达式我们很容易的推出类似 人吃饭。、天下雨。、猫抓鱼。 这样的句子。相信到这里小伙伴应该明白BNF范式的一些基本概念和使用方式了。我们再来插入一个题外话,既然这里提到BNF范式是一种上下文无关文法,那什么是上下文、什么是上下文无关。先别着急了解概念,我们仍然通过例子来说明。在上述的句子的定义中,我们一共可以生成 4 * 3 * 4 = 48 种 结果,我们可以获得类似 人吃饭。、猫抓鱼。这种有意义的句子,也可能产生像天吃鱼。、人下雨 这种读起来感觉别扭的非正常语句。但是在上下文无关的语法中,主语宾语和谓语的内容没有相互关联,也就是说谓语和宾语的产生与主语无关。那上下文有关的文法呢?这里为了产生一些有意义的句子,我们给它加上一些限定。例如人后面只能接 吃 抓作为谓语、而当吃作为谓语时只能将 饭、肉、鱼作为宾语。针对这种需求,我们可以进行如下定义<句子>::=<主语><谓语><宾语>。<主语>::=人|狗|猫|天人<谓语>::=人(吃|抓)吃<宾语>::=吃(饭|肉|鱼)这样我们对这个产生式进行了一些限定,当主语是人的时候,谓语只能产生吃和抓这样的宾语。这种情况下的描述就被称之为上下文有关。上下文无关我自己的理解就是后续表达式的产生不依赖前面已产生的内容。而上下文有关的含义则与之相法。这个上下文就跟我们这么多年阅读理解题里面写的“请根据上下文来理解某个词表达了作者怎样的心情”这里的上下文类似。当然更加规范的说法就是,在应用一个产生式进行推导时,前后已经推导出的部分结果就是上下文。上下文无关就是只要文法的定义里面有一个定义,不管前面的产生串是什么都可以应用相应的产生推导后面的内容。代码编写上面的定义只是开胃菜,希望通过上面的描述,小伙伴能够理解BNF范式的应用,至于上下文无关和上下文有关。这些暂时不用考虑,毕竟我们目前还是在做上下文无关文法相关的内容。这里我们要支持乘法和除法,首先要做的就是在 ETokenType 结构中添加对乘法和除法相关的定义typedef enum e_TokenType { CINT = 0, //整数 PLUS, //加法 MINUS, //减法 DIV, //乘法 MUL, //除法 END_OF_FILE // 字符串末尾结束符号 }ETokenType;接着在 get_next_token和 get_oper() 函数中添加对这两个运算符的支持// get_next_token else if (c == '*') { pToken->type = DIV; dyncstring_catch(&pToken->value, '*'); } else if (c == '/') { pToken->type = MUL; dyncstring_catch(&pToken->value, '/'); } // get_oper if (get_next_token(&token) && (token.type == PLUS || token.type == MINUS || token.type == DIV || token.type == MUL)) { oper = token.type; if (pRet) *pRet = true; }现在词法分析部分已经可以支持乘除法的符号解析了。接着来完成语法分析的部分。首先我们来定义一下这个简单计算器的文法。<expr>::=<term>{<oper><term>} <term>::={0|1|2|3|4|5|6|7|8|9} <oper>::=PLUS|MINUS|DIV|MUL回忆一下上一节给出的语法图,理解这个表达式并不算困难。但是这里我们定义的文法有一个问题,就是从文法上体现不出运算的优先级。学过小学数学的都知道算数运算中优先计算乘除法,最后算加减法。但是根据这个文法我们无法体现出乘除法的优先级。因此这里我们需要修改定义。优先计算乘除法在文法上可以理解成,乘除法单独成一个部分,我们获取这个部分的计算结果最后与其他部分一起计算加减法。用BNF范式来体现就是<expr>::=<term>{(PLUS|MINUS)<term>} <term>::=<factor>{(DIV|MUL)<factor>} <factor>::={0|1|2|3|4|5|6|7|8|9}与语法图类似,范式也可以很容易转化为代码。允许出现多次的我们在代码实现上体现为循环。而文法中相关的定义我们直接采用一些get方式来获取对应被打上标记的值即可。上述文法描述可以转化为如下的c 代码int expr() { bool bRet = false; int result = get_term(&bRet); int bEOF = false; do { ETokenType oper = get_oper(&bRet); switch (oper) { case PLUS: { int num = get_term(&bRet); if(bRet) result += num; } break; case MINUS: { int num = get_term(&bRet); if(bRet) result -= num; } break; case END_OF_FILE: printf("%d\n", result); bEOF = true; break; default: bRet = false; break; } } while (bRet && !bEOF); if (!bRet) { printf("Syntax Error!\n"); } return 0; }上述expr的定义就是由一个term加若干个 +|- 和后面的若干个term 来组成,因此这里有一个循环。来取出所有term 和所有加减法,并进行计算。int get_term(bool* pValid) { int result = get_factor(pValid); int bEOF = false; do { ETokenType oper = get_oper(pValid); switch (oper) { case DIV: { int num = get_factor(pValid); if (*pValid) result *= num; } break; case MUL: { int num = get_factor(pValid); if (*pValid) result /= num; } break; case PLUS: case MINUS: { g_pPosition--; bEOF = true; } break; case END_OF_FILE: { g_pPosition--; bEOF = true; } } } while (pValid && !bEOF); return result; }而term 则是由整数以及若干个乘除法和另一个整数组成,所以代码中也用循环来取一直到取到不是这个term 定义所组成的部。注意这里与之前一样,当取到term的结束部分,我们仍然需要将索引进行递减。而最终的oper 和 factor 则保持原来的算法不变。好了,本篇到此也就结束了,小伙伴可以到该位置 取出代码来进行阅读和修改。 -
 从0开始自制解释器——实现多个整数的加减法 在上一篇我们实现了一个可以计算两个多位整数加减法的计算器。本章我们继续来给这个计算器添加功能,这次要给它添加可以连续计算多个整数相加减的功能。例如我们可以计算 1 + 2 + 3 这样的表达式。语法图在正式写代码之前让我们先来学习一下一些基本的理论知识。这次要介绍的理论是语法图。什么是语法图呢?语法图是编程语言语法语法规则的图形表示。它体现了词法分析的运行规则。语法图直观的展示了在编程语言中哪些语句是符合语法的,哪些是不符合语法规范的。语法图的阅读非常容易,它类似于程序的流程图,只要顺着箭头指向的路径来读即可。与程序流程图类似,语法图中有些路径表示选择,有些表示循环。我们试着来读一下下面的语法图这张语法图表示的含义是,一个术语(term) 可选的跟上一个加号或者减号,而后面又需要跟上另一个术语。接着又可以有选择的跟上另一个加号或者减号。但是加号或者减号后面必须跟上另一个术语。这里又提到另一个单词,term 它的中文意思是术语。似乎很难用其他文字来解释何为术语。你只需要知道在这里它代表的是一个整数,它并不影响我们阅读这个语法图代码展示在上一篇中我们提到,将Token流识别为对应结构的过程被称之为词法分析,我们代码中的词法分析的实现主要在函数 expr 中。在这个函数中我们主要实现了词法分析以及最后的解释执行。我们按照语法图修改一下词法分析的代码我们先给出下面的伪代码获取第一个整数作为计算结果保存 while(解析到最后一个字符) { 获取操作符(+/-) switch(操作符) { case +: 获取下一个整数,如果不是整数则退出并报错 与结果相加 break; case -: 获取下一个整数,如果不是整数则退出并报错 与结果相减 break; } } 最终打印计算结果或者打印语法错误基于这个思路我们给出具体的实现代码int expr() { bool bRet = false; int result = get_term(&bRet); int bEOF = false; do { ETokenType oper = get_oper(&bRet); switch (oper) { case PLUS: { int num = get_term(&bRet); if(bRet) result += num; } break; case MINUS: { int num = get_term(&bRet); if(bRet) result -= num; } break; case END_OF_FILE: printf("%d\n", result); bEOF = true; break; default: bRet = false; break; } } while (bRet && !bEOF); if (!bRet) { printf("Syntax Error!\n"); } }这里为了便于理解,我将获取整数和操作符的模块又进行了一次封装,提供了两个函数分别是 get_term() 和 get_oper()。它们的代码如下int get_term(bool *pRet) { Token token = { 0 }; dyncstring_init(&token.value, DEFAULT_BUFFER_SIZE); int value = 0; if (get_next_token(&token) && token.type == CINT) { value = atoi(token.value.pszBuf); if (pRet) *pRet = true; } else { if (pRet) *pRet = false; } dyncstring_free(&token.value); return value; }ETokenType get_oper(bool* pRet) { Token token = { 0 }; dyncstring_init(&token.value, DEFAULT_BUFFER_SIZE); int oper = 0; if (get_next_token(&token) && (token.type == PLUS || token.type == MINUS)) { oper = token.type; if (pRet) *pRet = true; } else if (token.type == END_OF_FILE) { oper = END_OF_FILE; if (pRet) *pRet = true; } else { oper = -1; if (pRet) *pRet = false; } dyncstring_free(&token.value); return oper; }到此为止,就实现了多个整数的算术运算。整个实现过程的代码我都放到该位置。有兴趣的小伙伴可以自己对照着代码跟着我一起来实现属于自己的解释器。
从0开始自制解释器——实现多个整数的加减法 在上一篇我们实现了一个可以计算两个多位整数加减法的计算器。本章我们继续来给这个计算器添加功能,这次要给它添加可以连续计算多个整数相加减的功能。例如我们可以计算 1 + 2 + 3 这样的表达式。语法图在正式写代码之前让我们先来学习一下一些基本的理论知识。这次要介绍的理论是语法图。什么是语法图呢?语法图是编程语言语法语法规则的图形表示。它体现了词法分析的运行规则。语法图直观的展示了在编程语言中哪些语句是符合语法的,哪些是不符合语法规范的。语法图的阅读非常容易,它类似于程序的流程图,只要顺着箭头指向的路径来读即可。与程序流程图类似,语法图中有些路径表示选择,有些表示循环。我们试着来读一下下面的语法图这张语法图表示的含义是,一个术语(term) 可选的跟上一个加号或者减号,而后面又需要跟上另一个术语。接着又可以有选择的跟上另一个加号或者减号。但是加号或者减号后面必须跟上另一个术语。这里又提到另一个单词,term 它的中文意思是术语。似乎很难用其他文字来解释何为术语。你只需要知道在这里它代表的是一个整数,它并不影响我们阅读这个语法图代码展示在上一篇中我们提到,将Token流识别为对应结构的过程被称之为词法分析,我们代码中的词法分析的实现主要在函数 expr 中。在这个函数中我们主要实现了词法分析以及最后的解释执行。我们按照语法图修改一下词法分析的代码我们先给出下面的伪代码获取第一个整数作为计算结果保存 while(解析到最后一个字符) { 获取操作符(+/-) switch(操作符) { case +: 获取下一个整数,如果不是整数则退出并报错 与结果相加 break; case -: 获取下一个整数,如果不是整数则退出并报错 与结果相减 break; } } 最终打印计算结果或者打印语法错误基于这个思路我们给出具体的实现代码int expr() { bool bRet = false; int result = get_term(&bRet); int bEOF = false; do { ETokenType oper = get_oper(&bRet); switch (oper) { case PLUS: { int num = get_term(&bRet); if(bRet) result += num; } break; case MINUS: { int num = get_term(&bRet); if(bRet) result -= num; } break; case END_OF_FILE: printf("%d\n", result); bEOF = true; break; default: bRet = false; break; } } while (bRet && !bEOF); if (!bRet) { printf("Syntax Error!\n"); } }这里为了便于理解,我将获取整数和操作符的模块又进行了一次封装,提供了两个函数分别是 get_term() 和 get_oper()。它们的代码如下int get_term(bool *pRet) { Token token = { 0 }; dyncstring_init(&token.value, DEFAULT_BUFFER_SIZE); int value = 0; if (get_next_token(&token) && token.type == CINT) { value = atoi(token.value.pszBuf); if (pRet) *pRet = true; } else { if (pRet) *pRet = false; } dyncstring_free(&token.value); return value; }ETokenType get_oper(bool* pRet) { Token token = { 0 }; dyncstring_init(&token.value, DEFAULT_BUFFER_SIZE); int oper = 0; if (get_next_token(&token) && (token.type == PLUS || token.type == MINUS)) { oper = token.type; if (pRet) *pRet = true; } else if (token.type == END_OF_FILE) { oper = END_OF_FILE; if (pRet) *pRet = true; } else { oper = -1; if (pRet) *pRet = false; } dyncstring_free(&token.value); return oper; }到此为止,就实现了多个整数的算术运算。整个实现过程的代码我都放到该位置。有兴趣的小伙伴可以自己对照着代码跟着我一起来实现属于自己的解释器。 -
 从0开始自制解释器——实现多位整数的加减法计算器 上一篇我们实现了一个简单的加法计算器,并且了解了基本的词法分析、词法分析器的概念。本篇我们将要对之前实现的加法计算器进行扩展,我们为它添加以下几个功能计算减法能自动识别并跳过空白字符不再局限于单个整数,而是能计算多位整数提供一些工具函数首先为了支持减法,我们需要重新定义一下TokenType这个类型,也就是需要给 - 定义一个标志。现在我们的TokenType的定义如下typedef enum e_TokenType { CINT = 0, PLUS, MINUS, END_OF_FILE }ETokenType;由于需要支持多个整数,所以我们也不知道最终会有多少个字符,因此我们提供一个END_OF_FILE 表示我们访问到了最后一个字符,此时应该退出词法分析的过程。另外因为整数个数不再确定,我们也就不能按照之前的提供一个固定大小的数组。虽然可以提供一个足够大的空间来作为存储数字的缓冲,但是数字少了会浪费空间。而且考虑到之后要支持自定义变量和函数,采用固定长度缓冲的方式就很难找到合适的大小,太大显得浪费空间,太小有时候无法容纳得下用户定义的变量和函数名。因此这里我们采用动态长度的字符缓冲来保存。我们提供一个DyncString 的结构来保存这些内容#define DEFAULT_BUFFER_SIZE 16 // 动态字符串结构,用于保存任意长度的字符串 typedef struct DyncString { int nLength; // 字符长度 int capacity; //实际分配的空间大小 char* pszBuf; //保存字符串的缓冲 }DyncString, *LPDyncString; // 动态字符串初始化 // str: 被初始化的字符串 // size: 初始化字符串缓冲的大小,如果给0则按照默认大小分配空间 void dyncstring_init(LPDyncString str, int size); // 动态字符串空间释放 void dyncstring_free(LPDyncString str); //重分配动态字符串大小 void dyncstring_resize(LPDyncString str, int newSize); //往动态字符串中添加字符 void dyncstring_catch(LPDyncString str, char c); // 重置动态数组 void dyncstring_reset(LPDyncString str);它们的实现如下/*----------------------------动态数组的操作函数-------------------------------*/ void dyncstring_init(LPDyncString str, int size) { if (NULL == str) return; if (size == 0) str->capacity = DEFAULT_BUFFER_SIZE; else str->capacity = size; str->nLength = 0; str->pszBuf = (char*)malloc(sizeof(char) * str->capacity); if (NULL == str->pszBuf) { error("分配内存失败\n"); } memset(str->pszBuf, 0x00, sizeof(char) * str->capacity); } void dyncstring_free(LPDyncString str) { if (NULL == str) return; str->capacity = 0; str->nLength = 0; if (str->pszBuf == NULL) return; free(str->pszBuf); } void dyncstring_resize(LPDyncString str, int newSize) { int size = str->capacity; for (; size < newSize; size = size * 2); char* pszStr = (char*)realloc(str->pszBuf, size); str->capacity = size; str->pszBuf = pszStr; } void dyncstring_catch(LPDyncString str, char c) { if (str->capacity == str->nLength + 1) { dyncstring_resize(str, str->capacity + 1); } str->pszBuf[str->nLength] = c; str->nLength++; } void dyncstring_reset(LPDyncString str) { dyncstring_free(str); dyncstring_init(str, DEFAULT_BUFFER_SIZE); } /*----------------------------End 动态数组的操作函数-------------------------------*/另外提供一些额外的工具函数,他们的定义如下void error(char* lpszFmt, ...) { char szBuf[1024] = ""; va_list arg; va_start(arg, lpszFmt); vsnprintf(szBuf, 1024, lpszFmt, arg); va_end(arg); printf(szBuf); exit(-1); } bool is_digit(char c) { return (c >= '0' && c <= '9'); } bool is_space(char c) { return (c == ' ' || c == '\t' || c == '\r' || c == '\n'); }主要算法我们还是延续之前的算法,一个字符一个字符的解析,只是现在需要额外的将多个整数添加到一块作为一个整数处理。而且需要添加跳过空格的处理。首先我们对上次的代码进行一定程度的重构。我们添加一个函数专门用来获取下一个字符char get_next_char() { // 如果到达字符串尾部,索引不再增加 if (g_pPosition == '\0') { return '\0'; } else { char c = *g_pPosition; g_pPosition++; return c; } }expr() 函数里面大部分结构不变,主要算法仍然是按次序获取第一个整数、获取算术运算符、获取第二个整数。只是现在的整数都变成了采用 dyncstring 结构来存储int expr() { int val1 = 0, val2 = 0; Token token = { 0 }; dyncstring_init(&token.value, DEFAULT_BUFFER_SIZE); if (get_next_token(&token) && token.type == CINT) { val1 = atoi(token.value.pszBuf); } else { printf("首个操作数必须是整数\n"); dyncstring_free(&token.value); return -1; } int oper = 0; if (get_next_token(&token) && (token.type == PLUS || token.type == MINUS)) { oper = token.type; } else { printf("第二个字符必须是操作符, 当前只支持+/-\n"); dyncstring_free(&token.value); return -1; } if (get_next_token(&token) && token.type == CINT) { val2 = atoi(token.value.pszBuf); } else { printf("操作符后需要跟一个整数\n"); dyncstring_free(&token.value); return -1; } switch (oper) { case PLUS: { printf("%d+%d=%d\n", val1, val2, val1 + val2); } break; case MINUS: { printf("%d-%d=%d\n", val1, val2, val1 - val2); } break; default: printf("未知的操作!\n"); break; } dyncstring_free(&token.value); }最后就是最终要的 get_next_token 函数了。这个函数最主要的修改就是添加了解析整数和跳过空格的功能bool get_next_token(LPTOKEN pToken) { char c = get_next_char(); dyncstring_reset(&pToken->value); if (is_digit(c)) { dyncstring_catch(&pToken->value, c); pToken->type = CINT; parser_number(&pToken->value); } else if (c == '+') { pToken->type = PLUS; dyncstring_catch(&pToken->value, '+'); } else if (c == '-') { pToken->type = MINUS; dyncstring_catch(&pToken->value, '-'); } else if(is_space(c)) { skip_whitespace(); return get_next_token(pToken); } else if ('\0' == c) { pToken->type = END_OF_FILE; } else { return false; } return true; }在这个函数中我们先获取第一个字符,如果字符是整数则获取后面的整数并直接拼接为一个完整的整数。如果是空格则跳过接下来的空格。这两个是可能要处理多个字符所以这里使用了单独的函数来处理。其余只处理单个字符可以直接返回。parser_number 和 skip_whitespace 函数比较简单,主要的过程是不断从输入中取出字符,如果是空格则直接将索引往后移动,如果是整数则像对应的整数字符串中将整数字符加入。void skip_whitespace() { char c = '\0'; do { c = get_next_char(); } while (is_space(c)); // 遇到不是空白字符的,下次要取用它,这里需要重复取用上次取出的字符 g_pPosition--; } void parser_number(LPDyncString dyncstr) { char c = get_next_char(); while(is_digit(c)) { dyncstring_catch(dyncstr, c); c = get_next_char(); } // 遇到不是数字的,下次要取用它,这里需要重复取用上次取出的字符 g_pPosition--; }唯一需要注意的是,最后都有一个 g_pPosition-- 的操作。因为当我们发现下一个字符不符合条件的时候,它已经过了最后一个数字或者空格了,此时应该已经退回到get_next_token 函数中了,这个函数第一步就是获取下一个字符,因此会产生字符串被跳过的现象。所以这里我们执行 -- 退回到上一个位置,这样再取下一个就不会有问题了。最后为了能够获取空格的输入,我们将之前的scanf 改成 gets。这样就大功告成了。我们来测试一下结果最后的总结最后来一个总结。本篇我们对上一次的加法计算器进行了简单的改造,支持加减法、能跳过空格并且能够计算多位整数。在上一篇文章中,我们提到了Token,并且说过,像 get_next_token 这样给字符串每个部分打上Token的过程就是词法分析。get_next_token 这部分代码可以被称之为词法分析器。这篇我们再来介绍一下其他的概念。词位(lexeme): 词位的中文解释是语言词汇的基本单位。例如汉语的词位是汉字,英语的词位是基本的英文字母。对于我们这个加法计算器来说基本的词位就是数字以及 +\- 这两个符号parsing(语法分析)和 parser(语法分析器) 我们所编写的expr函数主要工作流程是根据token来组织代码行为。它的本质就是从Token流中识别出对应的结构,并将结构翻译为具体的行为。例如这里找到的结构是 CINT oper CINT。并且将两个int 按照 oper 指定的运算符进行算术运算。这个将Token流中识别出对应的结构的过程我们称之为语法分析,完成语法分析的组件被称之为语法分析器。expr 函数中即实现了语法分析的功能,也实现了解释执行的功能。
从0开始自制解释器——实现多位整数的加减法计算器 上一篇我们实现了一个简单的加法计算器,并且了解了基本的词法分析、词法分析器的概念。本篇我们将要对之前实现的加法计算器进行扩展,我们为它添加以下几个功能计算减法能自动识别并跳过空白字符不再局限于单个整数,而是能计算多位整数提供一些工具函数首先为了支持减法,我们需要重新定义一下TokenType这个类型,也就是需要给 - 定义一个标志。现在我们的TokenType的定义如下typedef enum e_TokenType { CINT = 0, PLUS, MINUS, END_OF_FILE }ETokenType;由于需要支持多个整数,所以我们也不知道最终会有多少个字符,因此我们提供一个END_OF_FILE 表示我们访问到了最后一个字符,此时应该退出词法分析的过程。另外因为整数个数不再确定,我们也就不能按照之前的提供一个固定大小的数组。虽然可以提供一个足够大的空间来作为存储数字的缓冲,但是数字少了会浪费空间。而且考虑到之后要支持自定义变量和函数,采用固定长度缓冲的方式就很难找到合适的大小,太大显得浪费空间,太小有时候无法容纳得下用户定义的变量和函数名。因此这里我们采用动态长度的字符缓冲来保存。我们提供一个DyncString 的结构来保存这些内容#define DEFAULT_BUFFER_SIZE 16 // 动态字符串结构,用于保存任意长度的字符串 typedef struct DyncString { int nLength; // 字符长度 int capacity; //实际分配的空间大小 char* pszBuf; //保存字符串的缓冲 }DyncString, *LPDyncString; // 动态字符串初始化 // str: 被初始化的字符串 // size: 初始化字符串缓冲的大小,如果给0则按照默认大小分配空间 void dyncstring_init(LPDyncString str, int size); // 动态字符串空间释放 void dyncstring_free(LPDyncString str); //重分配动态字符串大小 void dyncstring_resize(LPDyncString str, int newSize); //往动态字符串中添加字符 void dyncstring_catch(LPDyncString str, char c); // 重置动态数组 void dyncstring_reset(LPDyncString str);它们的实现如下/*----------------------------动态数组的操作函数-------------------------------*/ void dyncstring_init(LPDyncString str, int size) { if (NULL == str) return; if (size == 0) str->capacity = DEFAULT_BUFFER_SIZE; else str->capacity = size; str->nLength = 0; str->pszBuf = (char*)malloc(sizeof(char) * str->capacity); if (NULL == str->pszBuf) { error("分配内存失败\n"); } memset(str->pszBuf, 0x00, sizeof(char) * str->capacity); } void dyncstring_free(LPDyncString str) { if (NULL == str) return; str->capacity = 0; str->nLength = 0; if (str->pszBuf == NULL) return; free(str->pszBuf); } void dyncstring_resize(LPDyncString str, int newSize) { int size = str->capacity; for (; size < newSize; size = size * 2); char* pszStr = (char*)realloc(str->pszBuf, size); str->capacity = size; str->pszBuf = pszStr; } void dyncstring_catch(LPDyncString str, char c) { if (str->capacity == str->nLength + 1) { dyncstring_resize(str, str->capacity + 1); } str->pszBuf[str->nLength] = c; str->nLength++; } void dyncstring_reset(LPDyncString str) { dyncstring_free(str); dyncstring_init(str, DEFAULT_BUFFER_SIZE); } /*----------------------------End 动态数组的操作函数-------------------------------*/另外提供一些额外的工具函数,他们的定义如下void error(char* lpszFmt, ...) { char szBuf[1024] = ""; va_list arg; va_start(arg, lpszFmt); vsnprintf(szBuf, 1024, lpszFmt, arg); va_end(arg); printf(szBuf); exit(-1); } bool is_digit(char c) { return (c >= '0' && c <= '9'); } bool is_space(char c) { return (c == ' ' || c == '\t' || c == '\r' || c == '\n'); }主要算法我们还是延续之前的算法,一个字符一个字符的解析,只是现在需要额外的将多个整数添加到一块作为一个整数处理。而且需要添加跳过空格的处理。首先我们对上次的代码进行一定程度的重构。我们添加一个函数专门用来获取下一个字符char get_next_char() { // 如果到达字符串尾部,索引不再增加 if (g_pPosition == '\0') { return '\0'; } else { char c = *g_pPosition; g_pPosition++; return c; } }expr() 函数里面大部分结构不变,主要算法仍然是按次序获取第一个整数、获取算术运算符、获取第二个整数。只是现在的整数都变成了采用 dyncstring 结构来存储int expr() { int val1 = 0, val2 = 0; Token token = { 0 }; dyncstring_init(&token.value, DEFAULT_BUFFER_SIZE); if (get_next_token(&token) && token.type == CINT) { val1 = atoi(token.value.pszBuf); } else { printf("首个操作数必须是整数\n"); dyncstring_free(&token.value); return -1; } int oper = 0; if (get_next_token(&token) && (token.type == PLUS || token.type == MINUS)) { oper = token.type; } else { printf("第二个字符必须是操作符, 当前只支持+/-\n"); dyncstring_free(&token.value); return -1; } if (get_next_token(&token) && token.type == CINT) { val2 = atoi(token.value.pszBuf); } else { printf("操作符后需要跟一个整数\n"); dyncstring_free(&token.value); return -1; } switch (oper) { case PLUS: { printf("%d+%d=%d\n", val1, val2, val1 + val2); } break; case MINUS: { printf("%d-%d=%d\n", val1, val2, val1 - val2); } break; default: printf("未知的操作!\n"); break; } dyncstring_free(&token.value); }最后就是最终要的 get_next_token 函数了。这个函数最主要的修改就是添加了解析整数和跳过空格的功能bool get_next_token(LPTOKEN pToken) { char c = get_next_char(); dyncstring_reset(&pToken->value); if (is_digit(c)) { dyncstring_catch(&pToken->value, c); pToken->type = CINT; parser_number(&pToken->value); } else if (c == '+') { pToken->type = PLUS; dyncstring_catch(&pToken->value, '+'); } else if (c == '-') { pToken->type = MINUS; dyncstring_catch(&pToken->value, '-'); } else if(is_space(c)) { skip_whitespace(); return get_next_token(pToken); } else if ('\0' == c) { pToken->type = END_OF_FILE; } else { return false; } return true; }在这个函数中我们先获取第一个字符,如果字符是整数则获取后面的整数并直接拼接为一个完整的整数。如果是空格则跳过接下来的空格。这两个是可能要处理多个字符所以这里使用了单独的函数来处理。其余只处理单个字符可以直接返回。parser_number 和 skip_whitespace 函数比较简单,主要的过程是不断从输入中取出字符,如果是空格则直接将索引往后移动,如果是整数则像对应的整数字符串中将整数字符加入。void skip_whitespace() { char c = '\0'; do { c = get_next_char(); } while (is_space(c)); // 遇到不是空白字符的,下次要取用它,这里需要重复取用上次取出的字符 g_pPosition--; } void parser_number(LPDyncString dyncstr) { char c = get_next_char(); while(is_digit(c)) { dyncstring_catch(dyncstr, c); c = get_next_char(); } // 遇到不是数字的,下次要取用它,这里需要重复取用上次取出的字符 g_pPosition--; }唯一需要注意的是,最后都有一个 g_pPosition-- 的操作。因为当我们发现下一个字符不符合条件的时候,它已经过了最后一个数字或者空格了,此时应该已经退回到get_next_token 函数中了,这个函数第一步就是获取下一个字符,因此会产生字符串被跳过的现象。所以这里我们执行 -- 退回到上一个位置,这样再取下一个就不会有问题了。最后为了能够获取空格的输入,我们将之前的scanf 改成 gets。这样就大功告成了。我们来测试一下结果最后的总结最后来一个总结。本篇我们对上一次的加法计算器进行了简单的改造,支持加减法、能跳过空格并且能够计算多位整数。在上一篇文章中,我们提到了Token,并且说过,像 get_next_token 这样给字符串每个部分打上Token的过程就是词法分析。get_next_token 这部分代码可以被称之为词法分析器。这篇我们再来介绍一下其他的概念。词位(lexeme): 词位的中文解释是语言词汇的基本单位。例如汉语的词位是汉字,英语的词位是基本的英文字母。对于我们这个加法计算器来说基本的词位就是数字以及 +\- 这两个符号parsing(语法分析)和 parser(语法分析器) 我们所编写的expr函数主要工作流程是根据token来组织代码行为。它的本质就是从Token流中识别出对应的结构,并将结构翻译为具体的行为。例如这里找到的结构是 CINT oper CINT。并且将两个int 按照 oper 指定的运算符进行算术运算。这个将Token流中识别出对应的结构的过程我们称之为语法分析,完成语法分析的组件被称之为语法分析器。expr 函数中即实现了语法分析的功能,也实现了解释执行的功能。 -
 从0开始自制解释器——实现简单的加法计算器 为什么要学习编译器和解释器呢?文中的作者给出的答案有下面几个:为了深入理解计算机是如何工作的:一个显而易见的道理就是,如果你不懂编译器和解释器是如何工作的那么你就不明白计算机是如何工作的编译器和解释器用到的一些原理和编程技巧以及算法在其他地方也可以用到。学习编译器和解释器能够学到并强化这些技巧的运用为了方便日后能编写自己的编程语言或者专用领域的特殊语言接下来我们就从0开始一步一步的构建自己的解释器。跟着教程先制作一个简单的加法计算器,为了保证简单,这个加法计算器能够解析的表达式需要满足下面几点:目前只支持加法运算目前只支持两个10以内的整数的计算表达式之间不能有空格只能计算一次加法举一个例子来说,它可以计算诸如"1+2"、"5+6" 这样的表达式,但是不能计算像 "11+20"(必须是10以内)、"1.1+2"(需要两个数都是整数)、"1 + 2"(中间不能有空格)、"1+2+3"(只能计算一次加法)有了这些限制,我们很容易就能实现出来。实现的算法假设我们要计算表达式 5+6。这里主要的步骤是通过字符串保存表达式,然后通过索引依次访问每个字符,分别找到两个整数和加法运算符,最后实现两个整数相加的操作。第一步,我们的索引在表达式字符串的开始位置,解析得到当前位置的字符是一个整数,我们给它打上标记,类型为整形,值为5。第二步,索引向前推进,解析当前位置的字符是一个+。还是给它打上标记,类型为plus,值为+。第三步,索引继续前进,解析到当前位置的字符是一个整数,我们给它打上标记,类型为整形,值为6最后一步,根据得到的两个整数以及要执行的算术运算,我们将两个数直接进行相加得到最终结果具体的代码首先我们定义这个标记的类型,目前支持整数以及加法的标记typedef enum e_TokenType { CINT = 0, //整型 PLUS //加法运算符 }ETokenType; // 这里因为只支持10以内的整数,所以表示计算数字的字符只有一个,加上字符串最后的结束标记,字符数组只需要两个即可 typedef struct Token { ETokenType type; //类型 char value[2]; //值 }Token, *LPTOKEN;接着定义一些全局变量来保存算术运算的表达式和当前指针的索引char* g_pszUserBuf = NULL; char* g_pPosition = NULL;接着我们定义一个函数来模拟上述说到的不断解析每一个字符的过程bool get_next_token(LPTOKEN pToken) { char* sz = g_pPosition; g_pPosition++; pToken->value[0] = '\0'; if (*sz >= '0' && *sz <= '9') { pToken->type = CINT; pToken->value[0] = *sz; return true; } else if (*sz == '+') { pToken->type = PLUS; pToken->value[0] = *sz; return true; } else { pToken->value[0] = '\0'; return false; } }最后我们定义一个函数来执行获取每个标记并最终计算结果的操作int expr() { int val1 = 0, val2 = 0; Token token = { 0 }; if (get_next_token(&token) && token.type == CINT) { val1 = atoi(token.value); } else { printf("首个字符必须是整数"); return -1; } if (get_next_token(&token) && token.type == PLUS) { } else { printf("第二个字符必须是操作符,并且当前只支持 + 运算"); return -1; } if (get_next_token(&token) && token.type == CINT) { val2 = atoi(token.value); } printf("%d+%d=%d\n", val1, val2, val1 + val2); }在main函数里面我们只需要建立一个缓冲来保存字符,并且在循环中不断等待用户输入,完成解析并输出结果即可// 重制当前解析环境 void reset() { memset(g_pszUserBuf, 0x00, 16 * sizeof(char)); scanf_s("%s", g_pszUserBuf); g_pPosition = g_pszUserBuf; } int main() { g_pszUserBuf = (char*)malloc(16 * sizeof(char)); while (1) { printf(">>>"); reset(); if (strcmp(g_pszUserBuf, "exit") == 0) { break; } expr(); } return 0; }最终执行的结果如下最后的总结程序我们已经写完了,你可能觉得这个程序太简单了,只能做这点事情。别着急,后面将会逐步的去完善这个程序。以便它能实现更加复杂的运算。最后我们来引入一些概念性的东西:我们将输入内容按照一定规则打上的标记被称之为Token上述get_next_token函数体现的将一段字符串分割并打上有意义的标签的过程被称为词法分析。解释器工作的第一步就是将输入的字符串按照一定的规则转换为一系列有意义的标记。完成这个工作的组件被称之为词法分析器,也可以被称为扫描器或者分词器
从0开始自制解释器——实现简单的加法计算器 为什么要学习编译器和解释器呢?文中的作者给出的答案有下面几个:为了深入理解计算机是如何工作的:一个显而易见的道理就是,如果你不懂编译器和解释器是如何工作的那么你就不明白计算机是如何工作的编译器和解释器用到的一些原理和编程技巧以及算法在其他地方也可以用到。学习编译器和解释器能够学到并强化这些技巧的运用为了方便日后能编写自己的编程语言或者专用领域的特殊语言接下来我们就从0开始一步一步的构建自己的解释器。跟着教程先制作一个简单的加法计算器,为了保证简单,这个加法计算器能够解析的表达式需要满足下面几点:目前只支持加法运算目前只支持两个10以内的整数的计算表达式之间不能有空格只能计算一次加法举一个例子来说,它可以计算诸如"1+2"、"5+6" 这样的表达式,但是不能计算像 "11+20"(必须是10以内)、"1.1+2"(需要两个数都是整数)、"1 + 2"(中间不能有空格)、"1+2+3"(只能计算一次加法)有了这些限制,我们很容易就能实现出来。实现的算法假设我们要计算表达式 5+6。这里主要的步骤是通过字符串保存表达式,然后通过索引依次访问每个字符,分别找到两个整数和加法运算符,最后实现两个整数相加的操作。第一步,我们的索引在表达式字符串的开始位置,解析得到当前位置的字符是一个整数,我们给它打上标记,类型为整形,值为5。第二步,索引向前推进,解析当前位置的字符是一个+。还是给它打上标记,类型为plus,值为+。第三步,索引继续前进,解析到当前位置的字符是一个整数,我们给它打上标记,类型为整形,值为6最后一步,根据得到的两个整数以及要执行的算术运算,我们将两个数直接进行相加得到最终结果具体的代码首先我们定义这个标记的类型,目前支持整数以及加法的标记typedef enum e_TokenType { CINT = 0, //整型 PLUS //加法运算符 }ETokenType; // 这里因为只支持10以内的整数,所以表示计算数字的字符只有一个,加上字符串最后的结束标记,字符数组只需要两个即可 typedef struct Token { ETokenType type; //类型 char value[2]; //值 }Token, *LPTOKEN;接着定义一些全局变量来保存算术运算的表达式和当前指针的索引char* g_pszUserBuf = NULL; char* g_pPosition = NULL;接着我们定义一个函数来模拟上述说到的不断解析每一个字符的过程bool get_next_token(LPTOKEN pToken) { char* sz = g_pPosition; g_pPosition++; pToken->value[0] = '\0'; if (*sz >= '0' && *sz <= '9') { pToken->type = CINT; pToken->value[0] = *sz; return true; } else if (*sz == '+') { pToken->type = PLUS; pToken->value[0] = *sz; return true; } else { pToken->value[0] = '\0'; return false; } }最后我们定义一个函数来执行获取每个标记并最终计算结果的操作int expr() { int val1 = 0, val2 = 0; Token token = { 0 }; if (get_next_token(&token) && token.type == CINT) { val1 = atoi(token.value); } else { printf("首个字符必须是整数"); return -1; } if (get_next_token(&token) && token.type == PLUS) { } else { printf("第二个字符必须是操作符,并且当前只支持 + 运算"); return -1; } if (get_next_token(&token) && token.type == CINT) { val2 = atoi(token.value); } printf("%d+%d=%d\n", val1, val2, val1 + val2); }在main函数里面我们只需要建立一个缓冲来保存字符,并且在循环中不断等待用户输入,完成解析并输出结果即可// 重制当前解析环境 void reset() { memset(g_pszUserBuf, 0x00, 16 * sizeof(char)); scanf_s("%s", g_pszUserBuf); g_pPosition = g_pszUserBuf; } int main() { g_pszUserBuf = (char*)malloc(16 * sizeof(char)); while (1) { printf(">>>"); reset(); if (strcmp(g_pszUserBuf, "exit") == 0) { break; } expr(); } return 0; }最终执行的结果如下最后的总结程序我们已经写完了,你可能觉得这个程序太简单了,只能做这点事情。别着急,后面将会逐步的去完善这个程序。以便它能实现更加复杂的运算。最后我们来引入一些概念性的东西:我们将输入内容按照一定规则打上的标记被称之为Token上述get_next_token函数体现的将一段字符串分割并打上有意义的标签的过程被称为词法分析。解释器工作的第一步就是将输入的字符串按照一定的规则转换为一系列有意义的标记。完成这个工作的组件被称之为词法分析器,也可以被称为扫描器或者分词器 -
 从0开始自制解释器——综述 作为一个程序员,自制自己的编译器一直是一个梦想。之前也曾为了这个梦想学习过类似龙书、虎书这种大部头的书,但是光看理论总有一些云里雾里的感觉。看完只觉得脑袋昏昏沉沉并没有觉得有多少长进。当初看过《疯狂的程序员》这本书,书里说,真正能学会编译原理并不是靠看各种书然后通过相关考试,而是有一天你的领导找到你对你说:“小X啊,你是我们公司技术能力最强的人,咱们现在用的编译器性能有点跟不上,要不你看看能不能改进一下”。所以想要学习编译原理相关的知识首先要做的还是实践——实现一个自己的编译器。之前也看过类似的教你如何自制编译器,但是他们有一个共同的问题就是在很大程度上都借助第三方工具,隐藏了一些底层的细节。我希望的是每一行代码都是自己的完成的。所以一直怀揣着这个梦想直到最近我找到了一篇教程。一起写一个简单的编译器——魔力Python。这篇教程是实用Python完成的,但是这里我不打算使用Python,我打算实用最纯粹的C 语言来完成这个任务,我考虑使用C主要基于以下几个原因:Python 有一些封装的细节,不方便全方位的展示相关算法。原教程使用的就是Python,还用一样的话思路会受到教程的影响,要真正的理解需要自己一行行的敲代码,最好的方式就是用另一种语言来实现同样的算法现在市面上大多数都是用c来实现编译器,如果后续想要更近一步学习编译原理可以考虑在我完成的这版中很方便的加入一些新学的知识点自己有使用C的能力,而且用C写编译器自带装B属性基于以上理由,我准备开始跟着教程使用C来实现自己的解释器。这并不是一篇教程什么的,更多的是作为一篇实践笔记。而且根据我之前写的Vim专栏的经验来说,将它已专栏的形式发布出来之后鸽的可能性更小,更有动力来完成它。当然如果各位能从专栏中学到什么那就更好了。总之后面让我们一起进入学习编译原理的路程吧
从0开始自制解释器——综述 作为一个程序员,自制自己的编译器一直是一个梦想。之前也曾为了这个梦想学习过类似龙书、虎书这种大部头的书,但是光看理论总有一些云里雾里的感觉。看完只觉得脑袋昏昏沉沉并没有觉得有多少长进。当初看过《疯狂的程序员》这本书,书里说,真正能学会编译原理并不是靠看各种书然后通过相关考试,而是有一天你的领导找到你对你说:“小X啊,你是我们公司技术能力最强的人,咱们现在用的编译器性能有点跟不上,要不你看看能不能改进一下”。所以想要学习编译原理相关的知识首先要做的还是实践——实现一个自己的编译器。之前也看过类似的教你如何自制编译器,但是他们有一个共同的问题就是在很大程度上都借助第三方工具,隐藏了一些底层的细节。我希望的是每一行代码都是自己的完成的。所以一直怀揣着这个梦想直到最近我找到了一篇教程。一起写一个简单的编译器——魔力Python。这篇教程是实用Python完成的,但是这里我不打算使用Python,我打算实用最纯粹的C 语言来完成这个任务,我考虑使用C主要基于以下几个原因:Python 有一些封装的细节,不方便全方位的展示相关算法。原教程使用的就是Python,还用一样的话思路会受到教程的影响,要真正的理解需要自己一行行的敲代码,最好的方式就是用另一种语言来实现同样的算法现在市面上大多数都是用c来实现编译器,如果后续想要更近一步学习编译原理可以考虑在我完成的这版中很方便的加入一些新学的知识点自己有使用C的能力,而且用C写编译器自带装B属性基于以上理由,我准备开始跟着教程使用C来实现自己的解释器。这并不是一篇教程什么的,更多的是作为一篇实践笔记。而且根据我之前写的Vim专栏的经验来说,将它已专栏的形式发布出来之后鸽的可能性更小,更有动力来完成它。当然如果各位能从专栏中学到什么那就更好了。总之后面让我们一起进入学习编译原理的路程吧 -
 算法与数据结构(七):快速排序 在上一篇中,回顾了一下针对选择排序的优化算法——堆排序。堆排序的时间复杂度为O(nlogn),而快速排序的时间复杂度也是O(nlogn)。但是快速排序在同为O(n*logn)的排序算法中,效率也是相对较高的,而且快速排序使用了算法中一个十分经典的思想——分治法;因此掌握快速排序还是很有必要的。快速排序的基本思想如下:在一组无序元素中,找到一个数作为基准数。将大于它的数全部移动到它的右侧,小于它的全部移动到右侧。在分成的两个区中,再次重复1到2 的步骤,直到所有的数全部有序下面还是来看一个例子[3,6,1,2,8,4,7]首先选取一个基准数,一般选择序列最左侧的数为基准数,也就是3,将小于3的数移动到3的左边,大于3的移动到3的右边,得到如下的序列[2,1,3,6,8,4,7]接着针对左侧的[2, 1] 这个序列和 [6, 8, ,4, 7]这两个序列再次执行这种操作,直到所有的数都变为有序为止。知道了具体的思路下面就是写算法了。void QSort(int a[], int n) { int nIdx = adjust(a, 0, n -1); //针对调整之后的数据左右两侧序列都再次进行调整 if(nIdx != -1) { QSort(&a[0], nIdx); QSort(&a[nIdx + 1], n - nIdx - 1); } }这里定义了一个函数作为快速排序的函数,函数需要传入序列的首地址以及序列中间元素的长度。在排序函数中只需要关注如何进行调整即可。这里进行了一个判断,当调整函数返回-1时表示不需要调整,也就是说此时已经都是有序的了,这个时候就不需要调整了。程序的基本框架已经完成了,剩下的就是如何编写调整函数了。调整的算法如下:首先定义两个指针,指向最右侧和最左侧,最左侧指针指向基准数所在位置先从右往左扫描,当发现右侧数小于基准值时,将基准值位置的数替换为该数,并且立刻从左往右扫描,直到找到一个数大于基准值,再次进行替换接着再次从右往左扫描,直到找到小于基准数的值;并再次改变扫描顺序,直到调整完毕最后直到两个指针重合,此时重合的位置就是基准值所在位置根据这个思路,可以编写如下代码int QuickSort(int a[], int nLow, int nHigh) { if (nLow >= nHigh) { return -1; } int tmp = a[nLow]; int i = nLow; int j = nHigh; while (i != j) { //先从右往左扫描,只到找到比基准值小的数 //将该数放到基准值的左侧 while (a[j] > tmp && j > i) { j--; } if (a[j] < tmp) { a[i]= a[j]; i++; } //接着从左往右扫描,直到找到比基准值大的数 //将该数放入到基准值的右侧 while (a[i] < tmp && i < j) { i++; } if (a[i] > tmp) { a[j] = a[i]; j--; } } a[i] = tmp; return i; }到此已经完成了快速排序的算法编写了。在有大量的数据需要进行排序时快速排序的效果比较好,如果数据量小,或者排序的序列已经是一个逆序的有序序列,它退化成O(n^2)。快速排序是一个不稳定的排序算法。
算法与数据结构(七):快速排序 在上一篇中,回顾了一下针对选择排序的优化算法——堆排序。堆排序的时间复杂度为O(nlogn),而快速排序的时间复杂度也是O(nlogn)。但是快速排序在同为O(n*logn)的排序算法中,效率也是相对较高的,而且快速排序使用了算法中一个十分经典的思想——分治法;因此掌握快速排序还是很有必要的。快速排序的基本思想如下:在一组无序元素中,找到一个数作为基准数。将大于它的数全部移动到它的右侧,小于它的全部移动到右侧。在分成的两个区中,再次重复1到2 的步骤,直到所有的数全部有序下面还是来看一个例子[3,6,1,2,8,4,7]首先选取一个基准数,一般选择序列最左侧的数为基准数,也就是3,将小于3的数移动到3的左边,大于3的移动到3的右边,得到如下的序列[2,1,3,6,8,4,7]接着针对左侧的[2, 1] 这个序列和 [6, 8, ,4, 7]这两个序列再次执行这种操作,直到所有的数都变为有序为止。知道了具体的思路下面就是写算法了。void QSort(int a[], int n) { int nIdx = adjust(a, 0, n -1); //针对调整之后的数据左右两侧序列都再次进行调整 if(nIdx != -1) { QSort(&a[0], nIdx); QSort(&a[nIdx + 1], n - nIdx - 1); } }这里定义了一个函数作为快速排序的函数,函数需要传入序列的首地址以及序列中间元素的长度。在排序函数中只需要关注如何进行调整即可。这里进行了一个判断,当调整函数返回-1时表示不需要调整,也就是说此时已经都是有序的了,这个时候就不需要调整了。程序的基本框架已经完成了,剩下的就是如何编写调整函数了。调整的算法如下:首先定义两个指针,指向最右侧和最左侧,最左侧指针指向基准数所在位置先从右往左扫描,当发现右侧数小于基准值时,将基准值位置的数替换为该数,并且立刻从左往右扫描,直到找到一个数大于基准值,再次进行替换接着再次从右往左扫描,直到找到小于基准数的值;并再次改变扫描顺序,直到调整完毕最后直到两个指针重合,此时重合的位置就是基准值所在位置根据这个思路,可以编写如下代码int QuickSort(int a[], int nLow, int nHigh) { if (nLow >= nHigh) { return -1; } int tmp = a[nLow]; int i = nLow; int j = nHigh; while (i != j) { //先从右往左扫描,只到找到比基准值小的数 //将该数放到基准值的左侧 while (a[j] > tmp && j > i) { j--; } if (a[j] < tmp) { a[i]= a[j]; i++; } //接着从左往右扫描,直到找到比基准值大的数 //将该数放入到基准值的右侧 while (a[i] < tmp && i < j) { i++; } if (a[i] > tmp) { a[j] = a[i]; j--; } } a[i] = tmp; return i; }到此已经完成了快速排序的算法编写了。在有大量的数据需要进行排序时快速排序的效果比较好,如果数据量小,或者排序的序列已经是一个逆序的有序序列,它退化成O(n^2)。快速排序是一个不稳定的排序算法。 -
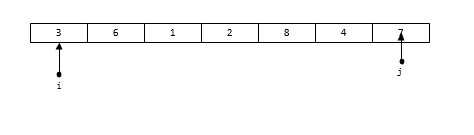
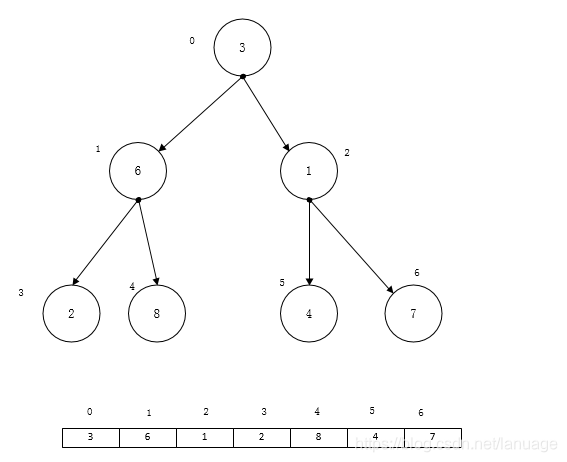
 算法与数据结构(六):堆排序 上一次说到了3种基本的排序算法,三种基本的排序算法时间复杂度都是O(n^2),虽然比较简单,但是效率相对较差,因此后续有许多相应的改进算法,这次主要说说堆排序算法。堆排序算法是对选择排序的一种优化。那么什么是堆呢?堆是一种树形结构。在维基百科上的定义是这样的“给定堆中任意节点 P 和 C,若 P 是 C 的母节点,那么 P 的值会小于等于(或大于等于) C 的值”。这句话通俗一点就是,树的根节点需要大于(小于)它的孩子节点,而每个左右子树都满足这个条件。当树的根节点大于它的左右孩子节点时称为大顶推,否则称为小顶堆。排序算法的思路是这样的,首先将序列中的元素组织成一个大顶堆,将树的根节点放到序列的最后面,然后将剩余的元素再组织成一个大顶堆,然后放到倒数第二个位置,以此类推。先假定它们的对应关系如下图所示:我们从树的最后一个非叶子节点开始,从这个子树中选择最大的一个数,将它交换到子树的根节点,也就是如下图所示接着再从后往前查找下一个非叶子节点经过这样一轮,一直调整到树的根节点,让后将根节点放到序列的最后一个元素,接着再将剩余元素重新组织为一个新的堆,直到所有元素都完成排序现在已经对堆排序的基本思路有了一定的了解,在写代码之前需要建立树节点与它在序列中的相关位置做一个对应关系,假设一个非叶子节点在序列中的位置为n,那么它的两个子节点分别是2n + 1与 2n + 2。而且小于n的一定是位于n前方的非叶子节点,所以在调整堆时,从n开始一直到0,前面的一定是非叶子节点,根据这点可以写出这样的代码void HeapSort(int a[], int nLength) { //从最后一个非叶子节点开始调整 for (int n = nLength / 2 - 1; n >= 0; n--) { HeapAdjust(a, n, nLength); } for (int n = nLength - 1; n > 0; n--) { //取堆顶与最后一个叶子节点互换 int tmp = a[0]; a[0] = a[n]; a[n] = tmp; //调整剩余堆 HeapAdjust(a, 0, n); } }上述代码首先取最后一个叶子节点,对所有非叶子节点进行调整,得到堆顶的最大元素。然后将最大元素与序列最后一个做交换,接着使用循环,对序列中剩余元素进行同样的操作。调整堆时,首先比较子树的根节点与它下面的所有子节点,并保存最大数的位置,然后将最大数与根节点的数进行交换,这样一直进行,直到完成了堆根节点的交换。void HeapAdjust(int a[], int nIdx, int nLength) { int child = 0; //child 保存当前最大数的下标 while (2 * nIdx + 1 < nLength) { child = 2 * nIdx + 1; //先找子节点的最大值(保证存在右节点的情况下) if (child < nLength - 1 && a[child] < a[child + 1]) { child++; } if (a[nIdx] < a[child]) { int tmp = a[nIdx]; a[nIdx] = a[child]; a[child] = tmp; }else { break; } //如果进行了交换,为了防止对子节点对应子树的破坏,要对子树也进行调整 nIdx = child; } }从算法上来看,它循环的次数与堆的深度有关,而二叉树的深度应该是log2(n) 向下取整,所以调整的时候需要进行log2(n)次调整,而外层需要从0一直到n - 1的位置每次都需要重组堆并进行调整,所以它的时间复杂度应该为O(nlogn), 它在效率上比选择排序要高,它的速度主要体现在每次查找选择最大的数这个方面。
算法与数据结构(六):堆排序 上一次说到了3种基本的排序算法,三种基本的排序算法时间复杂度都是O(n^2),虽然比较简单,但是效率相对较差,因此后续有许多相应的改进算法,这次主要说说堆排序算法。堆排序算法是对选择排序的一种优化。那么什么是堆呢?堆是一种树形结构。在维基百科上的定义是这样的“给定堆中任意节点 P 和 C,若 P 是 C 的母节点,那么 P 的值会小于等于(或大于等于) C 的值”。这句话通俗一点就是,树的根节点需要大于(小于)它的孩子节点,而每个左右子树都满足这个条件。当树的根节点大于它的左右孩子节点时称为大顶推,否则称为小顶堆。排序算法的思路是这样的,首先将序列中的元素组织成一个大顶堆,将树的根节点放到序列的最后面,然后将剩余的元素再组织成一个大顶堆,然后放到倒数第二个位置,以此类推。先假定它们的对应关系如下图所示:我们从树的最后一个非叶子节点开始,从这个子树中选择最大的一个数,将它交换到子树的根节点,也就是如下图所示接着再从后往前查找下一个非叶子节点经过这样一轮,一直调整到树的根节点,让后将根节点放到序列的最后一个元素,接着再将剩余元素重新组织为一个新的堆,直到所有元素都完成排序现在已经对堆排序的基本思路有了一定的了解,在写代码之前需要建立树节点与它在序列中的相关位置做一个对应关系,假设一个非叶子节点在序列中的位置为n,那么它的两个子节点分别是2n + 1与 2n + 2。而且小于n的一定是位于n前方的非叶子节点,所以在调整堆时,从n开始一直到0,前面的一定是非叶子节点,根据这点可以写出这样的代码void HeapSort(int a[], int nLength) { //从最后一个非叶子节点开始调整 for (int n = nLength / 2 - 1; n >= 0; n--) { HeapAdjust(a, n, nLength); } for (int n = nLength - 1; n > 0; n--) { //取堆顶与最后一个叶子节点互换 int tmp = a[0]; a[0] = a[n]; a[n] = tmp; //调整剩余堆 HeapAdjust(a, 0, n); } }上述代码首先取最后一个叶子节点,对所有非叶子节点进行调整,得到堆顶的最大元素。然后将最大元素与序列最后一个做交换,接着使用循环,对序列中剩余元素进行同样的操作。调整堆时,首先比较子树的根节点与它下面的所有子节点,并保存最大数的位置,然后将最大数与根节点的数进行交换,这样一直进行,直到完成了堆根节点的交换。void HeapAdjust(int a[], int nIdx, int nLength) { int child = 0; //child 保存当前最大数的下标 while (2 * nIdx + 1 < nLength) { child = 2 * nIdx + 1; //先找子节点的最大值(保证存在右节点的情况下) if (child < nLength - 1 && a[child] < a[child + 1]) { child++; } if (a[nIdx] < a[child]) { int tmp = a[nIdx]; a[nIdx] = a[child]; a[child] = tmp; }else { break; } //如果进行了交换,为了防止对子节点对应子树的破坏,要对子树也进行调整 nIdx = child; } }从算法上来看,它循环的次数与堆的深度有关,而二叉树的深度应该是log2(n) 向下取整,所以调整的时候需要进行log2(n)次调整,而外层需要从0一直到n - 1的位置每次都需要重组堆并进行调整,所以它的时间复杂度应该为O(nlogn), 它在效率上比选择排序要高,它的速度主要体现在每次查找选择最大的数这个方面。 -
 算法与数据结构(五):基本排序算法 前面几篇基本上把基本的数据结构都回顾完了,现在开始回顾那些常见的排序算法。排序是将一组无序的数据根据某种规则重新排列成有序的这么一个过程,当时在大学需要我们手工自己实现的主要有三种:选择排序、插入排序和冒泡排序。因为它比较简单,所以这里把他们放到一起作为最基本的排序算法。插入排序插入排序的思路是这样的:首先假设{k1, k2, k3, ...., kn} 中第一个元素是一个有序序列,从k2 开始插入到前面有序序列的适当位置从而使之前的有序序列仍然保持有序这么说可能有点抽象,我们以一个实例来说明:假设现在有这么一组待排元素: 3,6,1,2,8,4,7;先假设第一个元素3 是一个有序序列,从后续序列中取出6这个元素插入到前面的有序序列,得到3, 6 这么一个有序序列,此时序列为:3, 6, 1, 2, 8, 4, 7现在3, 6 是一个有序序列,从之前的序列中取出1,插入到有序序列的合适位置,得到1, 3, 6 这么一个有序序列,此时序列为: 1, 3, 6, 2, 8, 4, 7接着从待排元素中取出2,插入到适当位置,得到有序序列 1, 2, 3, 6;此时序列为 1, 2, 3, 6, 8, 4, 7以此类推,直到所有元素都排列完成,下面是每次排序后生成的序列1) 3 6 1 2 8 4 72) 1 3 6 2 8 4 73) 1 2 3 6 8 4 74) 1 2 3 6 8 4 75) 1 2 3 4 6 8 76) 1 2 3 4 6 7 87) 1 2 3 4 6 7 8那么知道了这个算法的思想,下面就是考虑该如何将其转化为代码,由计算机帮助我们实现这些事了。首先这段代码至少有一层循环来依次取出序列中的待排元素,由于假定第一个元素已经是有序的,所以循环次数应该是n - 1次,而且从序列的第2个元素开始。for(int i = 1; i < n; i++) { //do something; }那么如何确定元素的适当位置呢,我们人从肉眼上来看肯定是可以看出来的,计算机并不知道啊。由于之前的序列肯定是有序的,所以这里我们只需要从前往后将有序序列中的数与待插入数比较,只要序列中的数大于待插入数,那么将带插入数插入到该数的前面就可以了。因为之前的序列是有序的,插入到该位置肯定能保证新插入数大于它之前的数但是小于它之后的数。这个时候我们可以写出这样一段伪代码for(int i = i; i < n; i++) { for(int j = 0; j < i; j++) { if(a[i] < a[j]) { //此时j就是插入的位置,插入即可 } } }同时在插入的时候需要考虑腾挪后续的元素,为了方便腾挪元素,应该从有序列表的后方向前面进行比较,在比较的同时进行元素的腾挪,直到找到位置,这个时候的代码应该替换为这样for(int i = i; i < n; i++) { int tmp = a[i]; int j = i - 1; //从有序列表的最后一个元素开始往前找 while(j >= 0 && tmp < a[j]) { a[j + 1] = a[j]; //将对应元素往后挪一个位置 j--; } a[j + 1] = tmp; }从算法上来看,插入排序是一种O(n^2)的算法选择排序选择排序是最好理解的一种算法,选择排序的基本思路是每次从待排序列中选择最大(或者最小)的一个,放到已排好的序列的最前面,形成一个新的有序序列,直到所有元素都完成排序仍然是之前的一个序列 3, 6, 1, 2, 8, 4, 7首先找到最小的数1,排到最前面:1, 6, 3, 2, 8, 4, 7再找到后续最小数2,排到1后面:1, 2, 3, 6, 8, 4, 7接着找到后续最小数3,排到2后面:1, 2, 3, 6, 8, 4, 7以此类推,得到每次排序后的序列:1) 1 6 3 2 8 4 72) 1 2 3 6 8 4 73) 1 2 3 6 8 4 74) 1 2 3 4 8 6 75) 1 2 3 4 6 8 76) 1 2 3 4 6 7 87) 1 2 3 4 6 7 8从上面来看,每次确定了最小数之后只需要将对应位置的数与这个最小数交换就完成了排序,这也是与插入排序不同的地方,插入排序在处理元素的时候采用腾挪的方式,而选择排序则直接采用交换,也就是说插入排序在处理未排序元素的时候并没有改变他们的位置,而选择排序则有可能修改他们的位置,因此我们说选择排序是一种不稳定的排序,而插入排序是稳定的排序.实现的算法如下:for (int i = 0; i < n - 1; i++) { int k = i; //k 表示当前剩余序列中最小数的位置 //该循环从当前剩余数中找到最小数位置 for (int j = i; j < n; j++) { if (a[j] < a[k]) { k = j; } } if (k != i) { int tmp = a[k]; a[k] = a[i]; a[i] = tmp; } }选择排序的时间复杂度仍然是 O(n^2)冒泡排序冒泡排序是在C语言课上讲到的一种排序方式,简单来说就是将待排序列中的数据从头开始两两比较,然后将大数交换到后面,这样每次循环之后总是大数沉到最后面,进行多次这样的循环,就能完成排序还是从 3, 6, 1, 2, 8, 4, 7 序列的排序开始首先3与6相比,6大,此时不用交换,接着,6与1比较,6大然后进行交换。接着6与2比较,再交换,6与8比较,不用交换,8与4比较需要交换,8与7比较需要交换,因此第一次冒泡的结果是3, 1, 2, 6, 4, 7, 8依次类推得到每次结果如下:1) 3 1 2 6 4 7 82) 1 2 3 4 6 7 83) 1 2 3 4 6 7 84) 1 2 3 4 6 7 85) 1 2 3 4 6 7 86) 1 2 3 4 6 7 87) 1 2 3 4 6 7 8实现的算法如下:for (int i = 0; i < nLength - 1; i++) { for (int j = 0; j < nLength - i - 1; j++) { if (a[j] > a[j + 1]) { int tmp = a[j]; a[j] = a[j+ 1]; a[j + 1] = tmp; } } }冒泡排序也是一个不稳定的排序算法,它的时间复杂度也是O(n^2)
算法与数据结构(五):基本排序算法 前面几篇基本上把基本的数据结构都回顾完了,现在开始回顾那些常见的排序算法。排序是将一组无序的数据根据某种规则重新排列成有序的这么一个过程,当时在大学需要我们手工自己实现的主要有三种:选择排序、插入排序和冒泡排序。因为它比较简单,所以这里把他们放到一起作为最基本的排序算法。插入排序插入排序的思路是这样的:首先假设{k1, k2, k3, ...., kn} 中第一个元素是一个有序序列,从k2 开始插入到前面有序序列的适当位置从而使之前的有序序列仍然保持有序这么说可能有点抽象,我们以一个实例来说明:假设现在有这么一组待排元素: 3,6,1,2,8,4,7;先假设第一个元素3 是一个有序序列,从后续序列中取出6这个元素插入到前面的有序序列,得到3, 6 这么一个有序序列,此时序列为:3, 6, 1, 2, 8, 4, 7现在3, 6 是一个有序序列,从之前的序列中取出1,插入到有序序列的合适位置,得到1, 3, 6 这么一个有序序列,此时序列为: 1, 3, 6, 2, 8, 4, 7接着从待排元素中取出2,插入到适当位置,得到有序序列 1, 2, 3, 6;此时序列为 1, 2, 3, 6, 8, 4, 7以此类推,直到所有元素都排列完成,下面是每次排序后生成的序列1) 3 6 1 2 8 4 72) 1 3 6 2 8 4 73) 1 2 3 6 8 4 74) 1 2 3 6 8 4 75) 1 2 3 4 6 8 76) 1 2 3 4 6 7 87) 1 2 3 4 6 7 8那么知道了这个算法的思想,下面就是考虑该如何将其转化为代码,由计算机帮助我们实现这些事了。首先这段代码至少有一层循环来依次取出序列中的待排元素,由于假定第一个元素已经是有序的,所以循环次数应该是n - 1次,而且从序列的第2个元素开始。for(int i = 1; i < n; i++) { //do something; }那么如何确定元素的适当位置呢,我们人从肉眼上来看肯定是可以看出来的,计算机并不知道啊。由于之前的序列肯定是有序的,所以这里我们只需要从前往后将有序序列中的数与待插入数比较,只要序列中的数大于待插入数,那么将带插入数插入到该数的前面就可以了。因为之前的序列是有序的,插入到该位置肯定能保证新插入数大于它之前的数但是小于它之后的数。这个时候我们可以写出这样一段伪代码for(int i = i; i < n; i++) { for(int j = 0; j < i; j++) { if(a[i] < a[j]) { //此时j就是插入的位置,插入即可 } } }同时在插入的时候需要考虑腾挪后续的元素,为了方便腾挪元素,应该从有序列表的后方向前面进行比较,在比较的同时进行元素的腾挪,直到找到位置,这个时候的代码应该替换为这样for(int i = i; i < n; i++) { int tmp = a[i]; int j = i - 1; //从有序列表的最后一个元素开始往前找 while(j >= 0 && tmp < a[j]) { a[j + 1] = a[j]; //将对应元素往后挪一个位置 j--; } a[j + 1] = tmp; }从算法上来看,插入排序是一种O(n^2)的算法选择排序选择排序是最好理解的一种算法,选择排序的基本思路是每次从待排序列中选择最大(或者最小)的一个,放到已排好的序列的最前面,形成一个新的有序序列,直到所有元素都完成排序仍然是之前的一个序列 3, 6, 1, 2, 8, 4, 7首先找到最小的数1,排到最前面:1, 6, 3, 2, 8, 4, 7再找到后续最小数2,排到1后面:1, 2, 3, 6, 8, 4, 7接着找到后续最小数3,排到2后面:1, 2, 3, 6, 8, 4, 7以此类推,得到每次排序后的序列:1) 1 6 3 2 8 4 72) 1 2 3 6 8 4 73) 1 2 3 6 8 4 74) 1 2 3 4 8 6 75) 1 2 3 4 6 8 76) 1 2 3 4 6 7 87) 1 2 3 4 6 7 8从上面来看,每次确定了最小数之后只需要将对应位置的数与这个最小数交换就完成了排序,这也是与插入排序不同的地方,插入排序在处理元素的时候采用腾挪的方式,而选择排序则直接采用交换,也就是说插入排序在处理未排序元素的时候并没有改变他们的位置,而选择排序则有可能修改他们的位置,因此我们说选择排序是一种不稳定的排序,而插入排序是稳定的排序.实现的算法如下:for (int i = 0; i < n - 1; i++) { int k = i; //k 表示当前剩余序列中最小数的位置 //该循环从当前剩余数中找到最小数位置 for (int j = i; j < n; j++) { if (a[j] < a[k]) { k = j; } } if (k != i) { int tmp = a[k]; a[k] = a[i]; a[i] = tmp; } }选择排序的时间复杂度仍然是 O(n^2)冒泡排序冒泡排序是在C语言课上讲到的一种排序方式,简单来说就是将待排序列中的数据从头开始两两比较,然后将大数交换到后面,这样每次循环之后总是大数沉到最后面,进行多次这样的循环,就能完成排序还是从 3, 6, 1, 2, 8, 4, 7 序列的排序开始首先3与6相比,6大,此时不用交换,接着,6与1比较,6大然后进行交换。接着6与2比较,再交换,6与8比较,不用交换,8与4比较需要交换,8与7比较需要交换,因此第一次冒泡的结果是3, 1, 2, 6, 4, 7, 8依次类推得到每次结果如下:1) 3 1 2 6 4 7 82) 1 2 3 4 6 7 83) 1 2 3 4 6 7 84) 1 2 3 4 6 7 85) 1 2 3 4 6 7 86) 1 2 3 4 6 7 87) 1 2 3 4 6 7 8实现的算法如下:for (int i = 0; i < nLength - 1; i++) { for (int j = 0; j < nLength - i - 1; j++) { if (a[j] > a[j + 1]) { int tmp = a[j]; a[j] = a[j+ 1]; a[j + 1] = tmp; } } }冒泡排序也是一个不稳定的排序算法,它的时间复杂度也是O(n^2)