搜索到
15
篇与
的结果
-
 算法与数据结构(四):树 前面说的链表、栈、队列都是线性结构,而树是一个非线性节点。树简介树是一种非线性结构,由一个根节点和若干个子节点构成,每一个子节点又是一颗子树从定义上来看树的定义是一个递归的定义,树都有一个根节点,其中当根节点为空时它也是一颗特殊的树,树的示意图如下:相关术语树的度:树中各节点中最大的子节点数就是树的度,没有子节点的节点称为叶子节点节点的层次:从根节点开始,根节点的子节点为1层,子节点的子节点为第二层,依次类推树的深度:组成树的各节点的最大层数父节点与孩子节点:若一个节点有子节点,那么这个节点称为子节点的父节点,它的子节点称为它的孩子节点兄弟节点:具有相同父节点的节点互称为兄弟节点节点的祖先:从根到该节点所经分支上的所有节点子孙:以某节点为根的子树中任一节点都称为该节点的子孙二叉树对于树来说,并没有规定它能拥有几个子节点。一般常用的是节点数小于等于2的树,这种树一般称为二叉树。二叉树一般有如下几种形式空二叉树, 根节点为空只有一个节点的二叉树,只有根节点的二叉树只有左子树的二叉树只有右子树的二叉树完全二叉树满二叉树完全二叉树:若设二叉树的深度为h,除第 h 层外,其它各层 (1~(h-1)层) 的结点数都达到最大个数,第h层所有的结点都连续集中在最左边,这就是完全二叉树。也就是说除了最深层的非叶子节点,每层的子节点都必须有两个子节点,而且最后一层少节点只能最右边少。满二叉树: 一颗深度为h的二叉树,它的节点如果有2^k - 1 的话,它就是一颗满二叉树。也就说满二叉树是除了叶子节点,每个节点都有两个子节点的树完全二叉树的性质:$$在第k层,最多只有 2^(k -1) 个节点$$$$深度为k的完全二叉树,最多有 2^k - 2 个节点$$$$具有n个节点的完全二叉树的深度为\lfloor log_2(n)\rfloor $$二叉树的创建从上面的定义来看,树是一个递归的定义,因此在创建它的时候采用的也是递归的方式。树的节点暂时定义为:typedef struct _BTREE { int nVal; struct _BTREE *pLeft; struct _BTREE *pRight; }BTREE, *LPBTREE;树的节点中有两个节点指针,分别指向左子树和右子树。LPBTREE CreateBTree() { int n = 0; scanf_s("%d", &n); if (0 == n) { return NULL; } //创建节点本身 BTREE *t = (BTREE*)malloc(sizeof(BTREE)); if (NULL == t) { return NULL; } memset(t, 0x00, sizeof(BTREE)); t->nVal = n; printf("请输入%d的左子节点:", n); //递归调用函数来创建它的左子树 t->pLeft = CreateBTree(); //递归调用来创建它的右子树 printf("请输入%d的右子节点:", n); t->pRight = CreateBTree(); return t; }树的遍历树的遍历一般有三种方式,先序遍历、中序遍历、后序遍历先序遍历是先遍历根节点,在遍历它的左子树,最后遍历右子树,针对每颗子树都采用这种方式中序遍历是先遍历左子树,再遍历根节点,最后遍历右子树,针对每颗子树都采取这种方式遍历后续遍历是先遍历左子树,再遍历右子树,最后遍历根节点,针对每颗子树都采用这种方式遍历假设现在有一颗二叉树如下所示采用先序遍历得到的结果是:a、b、d、h、i、e、c、f、j、g、k采用中序遍历得到的结果是:h、d、i、b、e、a、j、f、c、g、k采用后续遍历得到的结果是:h、i、d、e、b、j、f、k、g、c、a根据数的结构我们知道它的先序遍历、中序遍历、后序遍历。同样的根据先序遍历,中序遍历或者根据后序遍历中序遍历可以得到一棵树的结构从而得到它的另一种遍历方式。这里需要注意的是根据先序遍历和后序遍历是不能唯一确定一颗树的假设现在有一棵二叉树先序遍历为a、b、d、g、h、k、e、i、c、f、j,中序遍历为:g、d、h、k、b、e、i、a、c、f、j 可以推断出它的树结构并得到后续遍历的结果。根据先序遍历a为第一个元素,可以得知a为根节点,再根据中序遍历中a的位置可以知道,g、d、h、k、b、e、i 为a的左子树,c、f、j为a的右子树。而且b c分别是左子树和右子树的根节点先来分析a的做子树,在先序遍历中,第一个元素为b,而中序遍历中b的位置可以知道g、d、h、k为左子树而e、i为右子树,而且g e分别是左子树和右子树的根节点以此类推可以得到a的左子树的布局大致如下:树的遍历也是一个递归的过程,将每个子节点看做一颗完整的树,再次调用遍历函数。只是根据不同的遍历方式,遍历函数调用的时机不同罢了//先序遍历 void PreOrder(LPBTREE pRoot) { if (NULL == pRoot) { return; } //先遍历根节点 printf("%d ", pRoot->nVal); //遍历左子树 PreOrder(pRoot->pLeft); //遍历右子树 PreOrder(pRoot->pRight); }//中序遍历 void InOrder(LPBTREE pRoot) { if (NULL == pRoot) { return; } InOrder(pRoot->pLeft); printf("%d ", pRoot->nVal); InOrder(pRoot->pRight); }//后续遍历 void PostOrder(LPBTREE pRoot) { if (NULL == pRoot) { return; } PostOrder(pRoot->pLeft); PostOrder(pRoot->pRight); printf("%d ", pRoot->nVal); }其他二叉树在算法中,二叉树应用的最为广泛,根据不同的用途,又可以分为这么几类二叉排序树:所有的左子树的节点都小于根节点,所有右子树的节点都大于根节点,而树的左右子树本身又是一颗二叉排序树;对于二叉排序树来说,中序遍历可以得到一个有序的集合。对于同一组有序的数值,生成的二叉排序树并不是唯一的,一般树的深度越浅,查找效率越高平衡二叉树:平衡二叉树是对二叉排序树的一种改进,平衡二叉树左右子树的高度差不超过1,其平衡因子定义为其左子树与右子树高度的差值,为了保持这个状态,每当插入一个数据时都需要对整个树做大量的调整。
算法与数据结构(四):树 前面说的链表、栈、队列都是线性结构,而树是一个非线性节点。树简介树是一种非线性结构,由一个根节点和若干个子节点构成,每一个子节点又是一颗子树从定义上来看树的定义是一个递归的定义,树都有一个根节点,其中当根节点为空时它也是一颗特殊的树,树的示意图如下:相关术语树的度:树中各节点中最大的子节点数就是树的度,没有子节点的节点称为叶子节点节点的层次:从根节点开始,根节点的子节点为1层,子节点的子节点为第二层,依次类推树的深度:组成树的各节点的最大层数父节点与孩子节点:若一个节点有子节点,那么这个节点称为子节点的父节点,它的子节点称为它的孩子节点兄弟节点:具有相同父节点的节点互称为兄弟节点节点的祖先:从根到该节点所经分支上的所有节点子孙:以某节点为根的子树中任一节点都称为该节点的子孙二叉树对于树来说,并没有规定它能拥有几个子节点。一般常用的是节点数小于等于2的树,这种树一般称为二叉树。二叉树一般有如下几种形式空二叉树, 根节点为空只有一个节点的二叉树,只有根节点的二叉树只有左子树的二叉树只有右子树的二叉树完全二叉树满二叉树完全二叉树:若设二叉树的深度为h,除第 h 层外,其它各层 (1~(h-1)层) 的结点数都达到最大个数,第h层所有的结点都连续集中在最左边,这就是完全二叉树。也就是说除了最深层的非叶子节点,每层的子节点都必须有两个子节点,而且最后一层少节点只能最右边少。满二叉树: 一颗深度为h的二叉树,它的节点如果有2^k - 1 的话,它就是一颗满二叉树。也就说满二叉树是除了叶子节点,每个节点都有两个子节点的树完全二叉树的性质:$$在第k层,最多只有 2^(k -1) 个节点$$$$深度为k的完全二叉树,最多有 2^k - 2 个节点$$$$具有n个节点的完全二叉树的深度为\lfloor log_2(n)\rfloor $$二叉树的创建从上面的定义来看,树是一个递归的定义,因此在创建它的时候采用的也是递归的方式。树的节点暂时定义为:typedef struct _BTREE { int nVal; struct _BTREE *pLeft; struct _BTREE *pRight; }BTREE, *LPBTREE;树的节点中有两个节点指针,分别指向左子树和右子树。LPBTREE CreateBTree() { int n = 0; scanf_s("%d", &n); if (0 == n) { return NULL; } //创建节点本身 BTREE *t = (BTREE*)malloc(sizeof(BTREE)); if (NULL == t) { return NULL; } memset(t, 0x00, sizeof(BTREE)); t->nVal = n; printf("请输入%d的左子节点:", n); //递归调用函数来创建它的左子树 t->pLeft = CreateBTree(); //递归调用来创建它的右子树 printf("请输入%d的右子节点:", n); t->pRight = CreateBTree(); return t; }树的遍历树的遍历一般有三种方式,先序遍历、中序遍历、后序遍历先序遍历是先遍历根节点,在遍历它的左子树,最后遍历右子树,针对每颗子树都采用这种方式中序遍历是先遍历左子树,再遍历根节点,最后遍历右子树,针对每颗子树都采取这种方式遍历后续遍历是先遍历左子树,再遍历右子树,最后遍历根节点,针对每颗子树都采用这种方式遍历假设现在有一颗二叉树如下所示采用先序遍历得到的结果是:a、b、d、h、i、e、c、f、j、g、k采用中序遍历得到的结果是:h、d、i、b、e、a、j、f、c、g、k采用后续遍历得到的结果是:h、i、d、e、b、j、f、k、g、c、a根据数的结构我们知道它的先序遍历、中序遍历、后序遍历。同样的根据先序遍历,中序遍历或者根据后序遍历中序遍历可以得到一棵树的结构从而得到它的另一种遍历方式。这里需要注意的是根据先序遍历和后序遍历是不能唯一确定一颗树的假设现在有一棵二叉树先序遍历为a、b、d、g、h、k、e、i、c、f、j,中序遍历为:g、d、h、k、b、e、i、a、c、f、j 可以推断出它的树结构并得到后续遍历的结果。根据先序遍历a为第一个元素,可以得知a为根节点,再根据中序遍历中a的位置可以知道,g、d、h、k、b、e、i 为a的左子树,c、f、j为a的右子树。而且b c分别是左子树和右子树的根节点先来分析a的做子树,在先序遍历中,第一个元素为b,而中序遍历中b的位置可以知道g、d、h、k为左子树而e、i为右子树,而且g e分别是左子树和右子树的根节点以此类推可以得到a的左子树的布局大致如下:树的遍历也是一个递归的过程,将每个子节点看做一颗完整的树,再次调用遍历函数。只是根据不同的遍历方式,遍历函数调用的时机不同罢了//先序遍历 void PreOrder(LPBTREE pRoot) { if (NULL == pRoot) { return; } //先遍历根节点 printf("%d ", pRoot->nVal); //遍历左子树 PreOrder(pRoot->pLeft); //遍历右子树 PreOrder(pRoot->pRight); }//中序遍历 void InOrder(LPBTREE pRoot) { if (NULL == pRoot) { return; } InOrder(pRoot->pLeft); printf("%d ", pRoot->nVal); InOrder(pRoot->pRight); }//后续遍历 void PostOrder(LPBTREE pRoot) { if (NULL == pRoot) { return; } PostOrder(pRoot->pLeft); PostOrder(pRoot->pRight); printf("%d ", pRoot->nVal); }其他二叉树在算法中,二叉树应用的最为广泛,根据不同的用途,又可以分为这么几类二叉排序树:所有的左子树的节点都小于根节点,所有右子树的节点都大于根节点,而树的左右子树本身又是一颗二叉排序树;对于二叉排序树来说,中序遍历可以得到一个有序的集合。对于同一组有序的数值,生成的二叉排序树并不是唯一的,一般树的深度越浅,查找效率越高平衡二叉树:平衡二叉树是对二叉排序树的一种改进,平衡二叉树左右子树的高度差不超过1,其平衡因子定义为其左子树与右子树高度的差值,为了保持这个状态,每当插入一个数据时都需要对整个树做大量的调整。 -
 算法与数据结构(三):栈 栈与队列一样也是一种线性的数据结构,与队列不同的是栈是一种先进后出的结构,有点类似于现实中的弹夹,最后压进去的子弹总是最先被打出来,在计算机中栈用到的地方就是用作函数传参与函数中局部变量的保存,也就是我们经常说的函数栈。栈同样有基于数组和基于链表的实现基于链表的实现基于链表实现的栈只需要一个头指针即可,插入删除都在头部进行。基于链表的栈没有栈满这一说,栈空的条件是头指针为NULL。元素入栈bool Push(int nValue) { LPSTACK_NODE p = (LPSTACK_NODE)malloc(sizeof(STACK_NODE)); if (NULL == p) { return false; } memset(p, 0x00, sizeof(STACK_NODE)); p->nVal = nValue; p->pNext = g_Top; g_Top = p; return true; }参数入栈是不需要判断栈是否为空的,不管是否为空,我们都采用同样的算法,即先使新节点的next指针域指向头,然后再重新给头指针赋值,由于不涉及到头指针所指向地址的访问,所以不需要额外判断头指针是否为空元素出栈元素出栈首先需要判断栈是否为空,如果不为空,则需要一个临时指针保存出栈元素,然后将头指针进行偏移bool Pop(int* pValue) { if (NULL == pValue) { return false; } if (IsStackEmpty()) { return false; } *pValue = g_Top->nVal; LPSTACK_NODE p = g_Top; g_Top = g_Top->pNext; free(p); return true; }基于数组实现的栈基于数组实现的栈也需要一个指针(或者在这里称之为下标),指向栈顶,在函数栈中这个充当栈顶指针的是一个寄存器ESP,而在函数栈中还有一个栈的基地址是ebp,基于数组的栈中,这个基地址就是数组的首地址。在基于数组实现的栈中,根据栈顶指针是否为0来判断。另外这种栈需要判断栈是否已满,一般采用的判断方式是判断栈顶指针是否为数组的最大长度。栈空、栈满判断bool IsStackEmpty() { return g_Top == 0; } bool IsStackFull() { return g_Top == MAX_SIZE; }根据不同的实现方式会有不同的判断方式,这里是让栈顶指针指向下一个即将入栈的元素所在的位置,如果栈顶指针指向的是当前栈顶元素的位置,那么这里可能需要改为 等于 -1来判断栈空,等于MAX_SIZE - 1来判断栈满元素入栈bool Push(int nValue) { if (IsStackFull()) { return false; } g_STACK[g_Top++] = nValue; return true; }元素出栈bool Pop(int* pValue) { if (NULL == pValue) { return false; } if (IsStackEmpty()) { return false; } *pValue = g_STACK[--g_Top]; return true; }由于栈都是在一端进行操作,所以不存在向队列那样有空间浪费,也不需要实现什么循环数组。从实现上来看栈比队列要简单的多。
算法与数据结构(三):栈 栈与队列一样也是一种线性的数据结构,与队列不同的是栈是一种先进后出的结构,有点类似于现实中的弹夹,最后压进去的子弹总是最先被打出来,在计算机中栈用到的地方就是用作函数传参与函数中局部变量的保存,也就是我们经常说的函数栈。栈同样有基于数组和基于链表的实现基于链表的实现基于链表实现的栈只需要一个头指针即可,插入删除都在头部进行。基于链表的栈没有栈满这一说,栈空的条件是头指针为NULL。元素入栈bool Push(int nValue) { LPSTACK_NODE p = (LPSTACK_NODE)malloc(sizeof(STACK_NODE)); if (NULL == p) { return false; } memset(p, 0x00, sizeof(STACK_NODE)); p->nVal = nValue; p->pNext = g_Top; g_Top = p; return true; }参数入栈是不需要判断栈是否为空的,不管是否为空,我们都采用同样的算法,即先使新节点的next指针域指向头,然后再重新给头指针赋值,由于不涉及到头指针所指向地址的访问,所以不需要额外判断头指针是否为空元素出栈元素出栈首先需要判断栈是否为空,如果不为空,则需要一个临时指针保存出栈元素,然后将头指针进行偏移bool Pop(int* pValue) { if (NULL == pValue) { return false; } if (IsStackEmpty()) { return false; } *pValue = g_Top->nVal; LPSTACK_NODE p = g_Top; g_Top = g_Top->pNext; free(p); return true; }基于数组实现的栈基于数组实现的栈也需要一个指针(或者在这里称之为下标),指向栈顶,在函数栈中这个充当栈顶指针的是一个寄存器ESP,而在函数栈中还有一个栈的基地址是ebp,基于数组的栈中,这个基地址就是数组的首地址。在基于数组实现的栈中,根据栈顶指针是否为0来判断。另外这种栈需要判断栈是否已满,一般采用的判断方式是判断栈顶指针是否为数组的最大长度。栈空、栈满判断bool IsStackEmpty() { return g_Top == 0; } bool IsStackFull() { return g_Top == MAX_SIZE; }根据不同的实现方式会有不同的判断方式,这里是让栈顶指针指向下一个即将入栈的元素所在的位置,如果栈顶指针指向的是当前栈顶元素的位置,那么这里可能需要改为 等于 -1来判断栈空,等于MAX_SIZE - 1来判断栈满元素入栈bool Push(int nValue) { if (IsStackFull()) { return false; } g_STACK[g_Top++] = nValue; return true; }元素出栈bool Pop(int* pValue) { if (NULL == pValue) { return false; } if (IsStackEmpty()) { return false; } *pValue = g_STACK[--g_Top]; return true; }由于栈都是在一端进行操作,所以不存在向队列那样有空间浪费,也不需要实现什么循环数组。从实现上来看栈比队列要简单的多。 -
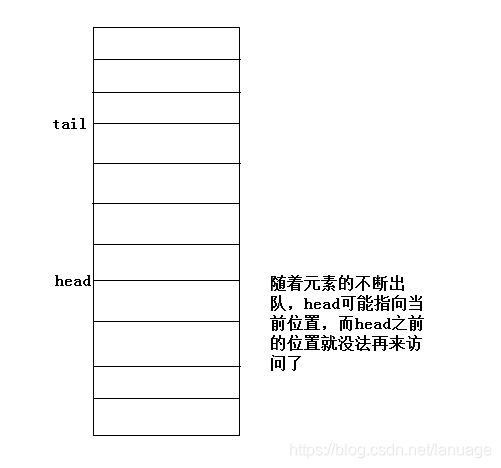
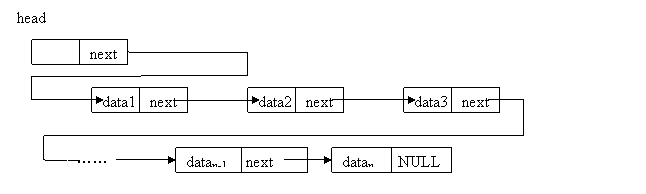
 算法与数据结构(二):队列 队列也是一种线性的数据结构,它与链表的区别在于链表可以在任意位置进行插入删除操作,而队列只能在一端进行插入,另一端进行删除。它对应于现实世界中的排队模型。队列有两种常见的实现方式:基于列表的实现和基于数组的实现基于链表的实现基于链表的队列,我们需要保存两个指针,一个指向头节点,一个指向尾节点。这种队列不存在队列满的情况,当然也可以根据业务需求给定一个最大值。当头结点为空时表示队列为空。由于队列只能在队尾插入数据,队首删除数据,因此针对队列的插入需要采用链表的尾插法,队列元素的出队需要改变头指针。队列节点的定义与链表节点的定义相同,下面给出各种操作的简单实现typedef struct _QNODE { int nValue; struct _QNODE *pNext; }QNODE, *LPQNODE; extern QNODE* g_front; extern QNODE* g_real;初始化初始化操作,我们简单的对两个指针进行赋值bool InitQueue() { g_front = g_real = NULL; return true; }元素入队元素入队的操作就是从队列尾部插入,当队列为空时,同时也是在队首插入元素,因此针对元素入队的操作,需要首先判断队列是否为空,为空时,需要针对队首和队尾指针进行赋值,而针对队列不为空的情况下,只需要改变队尾指针bool EnQueue(int nVal) { QNODE *p = (QNODE*)malloc(sizeof(QNO if (NULL == p) { return false; } memset(p, 0x00, sizeof(QNODE)); p->nValue = nVal; if (IsQueueEmpty()) //判断队列是否为空 { g_front = g_real = p; }else { g_real->pNext = p; g_real = p; } return true; }判断队列是否为空之前提到过,判断队列是否为空,只需要判断两个指针是否为空即可,因此这部分的代码如下:bool IsQueueEmpty() { return (g_front == NULL && g_real == NULL); }元素出队元素出队需要从队首出队,同样的需要判断队列是否为空。bool DeQueue(int *pVal) { if(NULL == pVal) { return false; } if (IsQueueEmpty()) { return false; } QNODE *p = g_front; //出队之后需要判断队列是否为空,以便针对队首、队尾指针进行赋值 if (NULL == g_front->pNext) { *pVal = g_front->nValue; g_front = NULL; g_real = NULL; }else { *pVal = g_front->nValue; g_front = g_front->pNext; } free(p); return true; } 基于数组的实现线性结构的队列也可以使用数组来实现,基于数组的实现也需要两个指针,分别是指向头部的下标和指向尾部的下标基于数组的实现中有这样一个问题,那就是内存资源的浪费问题。假设现在有一个能存储10个元素的队列,当前队列为空,随着元素的入队,此时队尾指针会一直向后偏移。当里面有部分元素的时候,来进行元素出队,这个时候队首指针会向后偏移。那么这个时候已经出队的位置在队列中再也访问不到了,但是它所占的内存仍然在那,这样就造成了内存空间的浪费,随着队列的不断使用,队列所能容纳的元素总数会不断减少。如图所示基于这种问题,我们采用循环数组的形式来表示一个队列,循环数组的结构大致如下图所示:这种队列的头指针不一定小于尾指针,当队首元素元素位于数组的尾部,这个时候只要数组中仍然有空闲位置来存储数据的时候,可以将队首指针再次指向数组的头部,从而实现空间的重复利用.在这种情况下队列的头部指针的计算公式为: head = (head + 1) % MAXSIZE,尾部的计算公式为 tail = (tail + 1) % MAXSIZE当队列为空时应该是 head == tail,注意,由于数组是循环数组,此时并不一定能保证它们二者都为0,只有当队列中从来没有过数据,也就是说是刚刚初始化完成的时候它们才都为0那么队列为满的情况又怎么确定呢?在使用普通数组的时候,当二者相等都为MAXSIZE的时候队列为满,但是在循环队列中,并不能根据二者都等于MAXSIZE来判断队列是否已满,有可能之前进行过出队的操作,所以在队列头之前的位置仍然能存数据,所以不能根据这个条件判断。那么是不是可以根据二者相等来判断呢?答案是不能,二者相等是用来判断队列为空的,那么怎么判断呢?这时候需要空出一块位置作为队尾的结束标志,回想一下给出的循环数组的实例图,每当head与tail只间隔一个元素的时候作为队列已满的标识。这个时候判断的公式为 (tail + 1) % MAXSIZE == head下面给出各种操作对应的代码队列的初始化int g_Queue[MAX_SIZE] = {0}; int g_front = 0; int g_real = 0; bool InitQueue() { g_front = g_real = 0; memset(g_Queue, 0x00, sizeof(g_Queue)); return true; } 入队bool EnQueue(int nVal) { if (IsQueueFull()) { return false; } g_Queue[g_real] = nVal; g_real = (g_real + 1) % MAX_SIZE; return true; }出队bool DeQueue(int *pVal) { if (NULL == pVal) { return false; } if (IsQueueFull()) { return false; } *pVal = g_Queue[g_front]; g_front = (g_front + 1) % MAX_SIZE; return true; }判断队空与队满bool IsQueueEmpty() { return g_real == g_front; } bool IsQueueFull() { return (( g_real + 1 ) % MAX_SIZE) == g_front; }最后从实现上来看基于数组的队列要比基于链表的简单许多,不需要考虑空指针,内存分配的问题,但是基于数组的队列需要额外考虑是否已满的情况,当然这个问题可以使用动态数组来避免。
算法与数据结构(二):队列 队列也是一种线性的数据结构,它与链表的区别在于链表可以在任意位置进行插入删除操作,而队列只能在一端进行插入,另一端进行删除。它对应于现实世界中的排队模型。队列有两种常见的实现方式:基于列表的实现和基于数组的实现基于链表的实现基于链表的队列,我们需要保存两个指针,一个指向头节点,一个指向尾节点。这种队列不存在队列满的情况,当然也可以根据业务需求给定一个最大值。当头结点为空时表示队列为空。由于队列只能在队尾插入数据,队首删除数据,因此针对队列的插入需要采用链表的尾插法,队列元素的出队需要改变头指针。队列节点的定义与链表节点的定义相同,下面给出各种操作的简单实现typedef struct _QNODE { int nValue; struct _QNODE *pNext; }QNODE, *LPQNODE; extern QNODE* g_front; extern QNODE* g_real;初始化初始化操作,我们简单的对两个指针进行赋值bool InitQueue() { g_front = g_real = NULL; return true; }元素入队元素入队的操作就是从队列尾部插入,当队列为空时,同时也是在队首插入元素,因此针对元素入队的操作,需要首先判断队列是否为空,为空时,需要针对队首和队尾指针进行赋值,而针对队列不为空的情况下,只需要改变队尾指针bool EnQueue(int nVal) { QNODE *p = (QNODE*)malloc(sizeof(QNO if (NULL == p) { return false; } memset(p, 0x00, sizeof(QNODE)); p->nValue = nVal; if (IsQueueEmpty()) //判断队列是否为空 { g_front = g_real = p; }else { g_real->pNext = p; g_real = p; } return true; }判断队列是否为空之前提到过,判断队列是否为空,只需要判断两个指针是否为空即可,因此这部分的代码如下:bool IsQueueEmpty() { return (g_front == NULL && g_real == NULL); }元素出队元素出队需要从队首出队,同样的需要判断队列是否为空。bool DeQueue(int *pVal) { if(NULL == pVal) { return false; } if (IsQueueEmpty()) { return false; } QNODE *p = g_front; //出队之后需要判断队列是否为空,以便针对队首、队尾指针进行赋值 if (NULL == g_front->pNext) { *pVal = g_front->nValue; g_front = NULL; g_real = NULL; }else { *pVal = g_front->nValue; g_front = g_front->pNext; } free(p); return true; } 基于数组的实现线性结构的队列也可以使用数组来实现,基于数组的实现也需要两个指针,分别是指向头部的下标和指向尾部的下标基于数组的实现中有这样一个问题,那就是内存资源的浪费问题。假设现在有一个能存储10个元素的队列,当前队列为空,随着元素的入队,此时队尾指针会一直向后偏移。当里面有部分元素的时候,来进行元素出队,这个时候队首指针会向后偏移。那么这个时候已经出队的位置在队列中再也访问不到了,但是它所占的内存仍然在那,这样就造成了内存空间的浪费,随着队列的不断使用,队列所能容纳的元素总数会不断减少。如图所示基于这种问题,我们采用循环数组的形式来表示一个队列,循环数组的结构大致如下图所示:这种队列的头指针不一定小于尾指针,当队首元素元素位于数组的尾部,这个时候只要数组中仍然有空闲位置来存储数据的时候,可以将队首指针再次指向数组的头部,从而实现空间的重复利用.在这种情况下队列的头部指针的计算公式为: head = (head + 1) % MAXSIZE,尾部的计算公式为 tail = (tail + 1) % MAXSIZE当队列为空时应该是 head == tail,注意,由于数组是循环数组,此时并不一定能保证它们二者都为0,只有当队列中从来没有过数据,也就是说是刚刚初始化完成的时候它们才都为0那么队列为满的情况又怎么确定呢?在使用普通数组的时候,当二者相等都为MAXSIZE的时候队列为满,但是在循环队列中,并不能根据二者都等于MAXSIZE来判断队列是否已满,有可能之前进行过出队的操作,所以在队列头之前的位置仍然能存数据,所以不能根据这个条件判断。那么是不是可以根据二者相等来判断呢?答案是不能,二者相等是用来判断队列为空的,那么怎么判断呢?这时候需要空出一块位置作为队尾的结束标志,回想一下给出的循环数组的实例图,每当head与tail只间隔一个元素的时候作为队列已满的标识。这个时候判断的公式为 (tail + 1) % MAXSIZE == head下面给出各种操作对应的代码队列的初始化int g_Queue[MAX_SIZE] = {0}; int g_front = 0; int g_real = 0; bool InitQueue() { g_front = g_real = 0; memset(g_Queue, 0x00, sizeof(g_Queue)); return true; } 入队bool EnQueue(int nVal) { if (IsQueueFull()) { return false; } g_Queue[g_real] = nVal; g_real = (g_real + 1) % MAX_SIZE; return true; }出队bool DeQueue(int *pVal) { if (NULL == pVal) { return false; } if (IsQueueFull()) { return false; } *pVal = g_Queue[g_front]; g_front = (g_front + 1) % MAX_SIZE; return true; }判断队空与队满bool IsQueueEmpty() { return g_real == g_front; } bool IsQueueFull() { return (( g_real + 1 ) % MAX_SIZE) == g_front; }最后从实现上来看基于数组的队列要比基于链表的简单许多,不需要考虑空指针,内存分配的问题,但是基于数组的队列需要额外考虑是否已满的情况,当然这个问题可以使用动态数组来避免。 -
 算法与数据结构(二):链表 上一篇简单的开了一个头,简单介绍了一下所谓的时间复杂度与空间复杂度,从这篇开始将陆陆续续写一下常用的数据结构:链表、队列、栈、树等等。链表当初是我在学校时唯一死磕过的数据结构,那个时候自己还算是一个好学生,虽然上课没怎么听懂,但是课后还是根据仔细调试过老师给的代码,硬是自己给弄懂了,它是我离校时唯一能够写出实现的数据结构,现在回想起来应该是它比较简单,算法也比较直来直去吧。虽然它比较简单,很多朋友也都会链表。但是作为一个系列,如果仅仅因为它比较简单而不去理会,总觉得少了点什么,所以再这仍然将其列举出来。单向链表单向链表是链表中的一种,它的特点是只有一个指向下一个节点的指针域,对单向链表的访问需要从头部开始,根据指针域依次访问下一个节点,单向链表的结构如下图所示单向链表的创建单向链表的结构只需要一个数据域与指针域,这个数据域可以是一个结构体,也可以是多个基本数据类型;指针域是一个指向节点类型的指针,简单的定义如下:typedef struct _LIST_NODE { int nVal; struct _LIST_NODE *pNext; }LIST_NODE, *LPLIST_NODE;创建链表可以采用头插法或者尾插法来初始化一个有多个节点的链表头插法的示意图如下:它的过程就像示意图中展现的,首先使用新节点p的next指针指向当前的头节点把新节点加入到链表头,然后变更链表头指针,这样就在头部插入了一个节点,用代码来展示就是p->next = head; head = p;我们使用一个函数来封装就是LPLIST_NODE CreateListHead() { LPLIST_NODE pHead = NULL; while (TRUE) { LPLIST_NODE p = (LPLIST_NODE)malloc(sizeof(LIST_NODE)); if (NULL == p) { break; } memset(p, 0x00, sizeof(LIST_NODE)); printf("请输入节点值(为0时将退出创建节点):"); scanf_s("%d", &p->nVal); //这里不需要对链表为空单独讨论 //当链表为空时pHead 的值为NULL, 这两句代码就变为 //p->pNext = NULL; //pHead = p; p->pNext = pHead; pHead = p; if (p->nVal == 0) { break; } } return pHead; }采用尾插法的话,首先得获得链表的尾部 pTail, 然后使尾节点的next指针指向新节点,然后更新尾节点,用代码来表示就是pTail->next = p; pTail = p;下面的函数是采用尾插法来构建链表的例子//这个函数多定义了一个变量用来保存 // 可以不需要这个变量,这样在插入之前需要遍历一遍链表,以便找到尾节点 // 但是每次插入之前都需要遍历一遍,没有定义一个变量保存尾节点这种方式来的高效 LPLIST_NODE CreateListTail() { LPLIST_NODE pHead = NULL; LPLIST_NODE pTail = pHead; while (NULL != pTail && NULL != pTail->pNext) { pTail = pTail->pNext; } while (TRUE) { LPLIST_NODE p = (LPLIST_NODE)malloc(sizeof(LIST_NODE)); if (NULL == p) { break; } memset(p, 0x00, sizeof(LIST_NODE)); printf("请输入节点值(为0时将退出创建节点):"); scanf_s("%d", &p->nVal); //由于这种方法需要对尾节点的next域赋值,所以需要考虑链表为空的情况 if (NULL == pTail) { pHead = p; pTail = pHead; }else { pTail->pNext = p; pTail = p; } if (p->nVal == 0) { break; } } return pHead; }链表的遍历链表的每个节点在内存中不是连续的,所以它不能像数组那样根据下标来访问(当然可以利用C++中的运算符重载来实现使用下标访问),链表中的每一个节点都保存了下一个节点的地址,所以我们根据每个节点指向的下一个节点来依次访问每个节点,访问的代码如下:void TraverseList(LPLIST_NODE pHead) { while (NULL != pHead) { printf("%d\n", pHead->nVal); pHead = pHead->pNext; } }链表的删除链表的每个节点都是在堆上分配的,在不再使用的时候需要手工清除每个节点。清除时需要使用遍历的方法,一个个的删除,只是需要在遍历的指针移动到下一个节点前保存当前节点,以便能够删除当前节点,删除的函数如下void DestroyList(LPLIST_NODE pHead) { LPLIST_NODE pTmp = pHead; while (NULL != pTmp) { pTmp = pHead->pNext; delete pHead; pHead = pTmp; } }删除单个节点如上图所示,假设我们要删除q节点,那么首先需要遍历找到q的上一个节点p,将p的next指针指向q的下一个节点,也就是赋值为q的next指针的值,用代码表示就是p->next = q->next;删除节点的函数如下:void DeleteNode(LPLIST_NODE* ppHead, int nValue) { if (NULL == ppHead || NULL == *ppHead) { return; } LPLIST_NODE p, q; p = *ppHead; while (NULL != p) { if (nValue == p->nVal) { if (*ppHead == p) { *ppHead = p->pNext; free(p); }else { q->pNext = p->pNext; free(p); } p = NULL; q = NULL; break; } q = p; p = p->pNext; } }在上述代码中首先来遍历链表,找到要删除的节点p和它的上一个节点q,由于头节点没有上一个节点,所以需要特别判断一下需要删除的是否为头节点,如果为头结点,则直接将头指针指向它的下一个节点,然后删除头结点即可,如果不是则采用之前的方法来删除。任意位置插入节点如上图所示,如果需要在q节点之后插入p节点的话,需要两步,将q的next节点指向q,然后将q指向之前p的下一个节点,这个时候需要注意一下顺序,如果我们先执行q->next = p 的话,那么之前q的下一个节点的地址就被覆盖掉了,这个时候后面的节点都丢掉了,所以这里我们要先执行p->next = q->next 这条语句,然后在执行q->next = p下面是一个创建有序链表的例子,这个例子演示了在任意位置插入节点LPLIST_NODE CreateSortedList() { LPLIST_NODE pHead = NULL; while (TRUE) { LPLIST_NODE p = (LPLIST_NODE)malloc(sizeof(LIST_NODE)); if (NULL == p) { break; } memset(p, 0x00, sizeof(LIST_NODE)); printf("请输入节点值(为0时将退出创建节点):"); scanf_s("%d", &p->nVal); if (NULL == pHead) { pHead = p; }else { if (pHead->nVal > p->nVal) { p->pNext = pHead; pHead = p; }else { LPLIST_NODE q = pHead; LPLIST_NODE r = q; q = q->pNext; while (NULL != q && q->nVal < p->nVal) { r = q; q = q->pNext; } p->pNext = r->pNext; r->pNext = p; } } if (p->nVal == 0) { break; } } return pHead; }当确定新节点的值之后,首先遍历链表,直到找到比新节点中数值大的节点,那么这个新节点就是需要插入到该节点之前。在遍历的时候使用r来保存之前的节点。这里需要注意这些情况:链表为空:这种情况下,直接让头指针指向当前节点如果头节点本身就是大于新节点的值,这种情况下采用头插法,将新节点插入到头部如果链表中未找到比新节点的值更大的值,这种情况下直接采用尾插发在链表中找到比新节点值更大的节点,这种情况下,在链表中插入但是在代码中并没有考虑到尾部插入的情况,由于在尾部插入时,r等于尾节点,r->pNext 的值为NULL, 所以 p->pNext = r->pNext;r->pNext = p; 可以看成 p->pNext = NULL; r->pNext = p; 也就是将p的next指针指向空,让其作为尾节点,将之前的尾节点的next指针指向新节点。循环链表循环链表是建立在单向链表的基础之上的,循环链表的尾节点并不指向空,而是指向其他的节点,可以是头结点,可以是自身,也可以是链表中的其他节点,为了方便操作,一般将循环链表的尾节点的next指针指向头节点,它的操作与单链表的操作类似,只需要将之前判断尾节点的条件变为 pTail->pNext == pHead 即可。这里就不再详细分析每种操作了,直接给出代码LPLIST_NODE CreateLoopList() { LPLIST_NODE pHead = NULL; LPLIST_NODE pTail = pHead; while(1) { LPLIST_NODE p = (LPLIST_NODE)malloc(sizeof(LIST_NODE)); if (NULL == p) { break; } memset(p, 0x00, sizeof(LIST_NODE)); printf("请输入一个值:"); scanf_s("%d", &p->nVal); if (NULL == pHead) { pHead = p; p->pNext = pHead; pTail = pHead; }else { pTail->pNext = p; p->pNext = pHead; pTail = p; } if (0 == p->nVal) { break; } } return pHead; } void TraverseLoopList(LPLIST_NODE pHead) { LPLIST_NODE pTmp = pHead; if (NULL == pTmp) { return; } do { printf("%d, ", pTmp->nVal); pTmp = pTmp->pNext; } while (pTmp != pHead); } void DestroyLoopList(LPLIST_NODE pHead) { LPLIST_NODE pTmp = pHead; LPLIST_NODE pDestroy = pTmp; if (NULL == pTmp) { return; } do { pTmp = pDestroy->pNext; free(pDestroy); pDestroy = pTmp; }while (pHead != pTmp); }判断链表是否为循环链表在上面说过,循环链表的尾指针不一定指向头节点,它可以指向任何节点,那么该怎么判断一个节点是否为循环链表呢?既然它可以指向任意的节点,那么肯定是找不到尾节点的,而且堆内存的分配是随机的,我们也不可能按照指针变量的大小来判断哪个节点在前哪个在后。回想一下在学校跑一千米的时候是不是回出现这样的情况,跑的块的会领先跑的慢的一周?根据这种情形我们可以考虑使用这样一种办法:定义两个指针,一个一次走两步也是就是p = p->next->next, 一个慢指针一次走一步,也就是q = q->next,如果是循环链表,那么快指针在某个时候一定会领先慢指针一周,也就是达到 p == q 这个条件,否则就是非循环链表。根据这个思路,可以考虑写下如下代码:bool IsLoopList(LPLIST_NODE pHead) { if (NULL == pHead) { return false; } LPLIST_NODE p = pHead; LPLIST_NODE q = pHead->pNext; while (NULL != p && NULL != q && NULL != q->pNext && p != q) { p = p->pNext; q = q->pNext->pNext; } if (q == NULL || NULL == p || NULL == q->pNext) { return false; } return true; }双向链表之前在插入或者删除的时候,需要定义两个指针变量,让其中一个一直更在另一个的后面,单向链表有一个很大的问题,不能很方便的找到它的上一个节点,为了解决这一个问题,提出了双向链表,双向链表与单向相比,多了一个指针域,用来指向它的上一个节点,也就是如下图所示:双向链表的操作与单向链表的类似,只是多了一个指向前一个节点的指针域,它要考虑的情况与单向链表相似删除节点删除节点的示意图如下:假设删除的节点p,那么首先根据p的pre指针域,找到它的上一个节点q,采用与单向链表类似的操作:q->next = p->next; p->next->pre = q;下面是删除节点的例子:void DeleteDNode(LPDLIST_NODE* ppHead, int nValue) { if (NULL == ppHead || NULL == *ppHead) { return; } LPDLIST_NODE p = *ppHead; while (NULL != p && p->nVal != nValue) { p = p->pNext; } if (NULL == p) { return; } if (*ppHead == p) { *ppHead = (*ppHead)->pNext; p->pPre = NULL; free(p); } else if (p->pNext == NULL) { p->pPre->pNext = NULL; free(p); }else { p->pPre->pNext = p->pNext; p->pNext->pPre = p->pPre; } }插入节点插入节点的示意图如下:假设新节点为p,插入的位置为q,则插入操作可以进行如下操作p->next = q->next; p->pre = q; q->next->pre = p; q->next = p;也是一样要考虑不能覆盖q的next指针域否则可能存在找不到原来链表中q的下一个节点的情况。所以这里先对p的next指针域进行操作下面也是采用创建有序列表的例子LPDLIST_NODE CreateSortedDList() { LPDLIST_NODE pHead = NULL; while (1) { LPDLIST_NODE pNode = (LPDLIST_NODE)malloc(sizeof(DLIST_NODE)); if (NULL == pNode) { return pHead; } memset(pNode, 0x00, sizeof(DLIST_NODE)); printf("请输入一个整数:"); scanf_s("%d", &pNode->nVal); if(NULL == pHead) { pHead = pNode; }else { LPDLIST_NODE q = pHead; LPDLIST_NODE r = q; while (NULL != q && q->nVal < pNode->nVal) { r = q; q = q->pNext; } if (q == pHead) { pNode->pNext = pHead; pHead->pPre = pNode; pHead = pNode; }else if (NULL == q) { r->pNext = pNode; pNode->pPre = r; }else { pNode->pPre = r; pNode->pNext = q; r->pNext = pNode; q->pPre = pNode; } } LPDLIST_NODE q = pHead; LPDLIST_NODE r = q; if (0 == pNode->nVal) { break; } } return pHead; }链表还有一种是双向循环链表,对于这种链表主要是在双向链表的基础上,将头结点的pre指针指向某个节点,将尾节点的next节点指向某个节点,而且这两个指针可以指向同一个节点也可以指向不同的节点,一般在使用中都是head的pre节点指向尾节点,而tail的next节点指向头节点。这里就不再详细说明,这些链表只要掌握其中一种,剩下的很好掌握的。
算法与数据结构(二):链表 上一篇简单的开了一个头,简单介绍了一下所谓的时间复杂度与空间复杂度,从这篇开始将陆陆续续写一下常用的数据结构:链表、队列、栈、树等等。链表当初是我在学校时唯一死磕过的数据结构,那个时候自己还算是一个好学生,虽然上课没怎么听懂,但是课后还是根据仔细调试过老师给的代码,硬是自己给弄懂了,它是我离校时唯一能够写出实现的数据结构,现在回想起来应该是它比较简单,算法也比较直来直去吧。虽然它比较简单,很多朋友也都会链表。但是作为一个系列,如果仅仅因为它比较简单而不去理会,总觉得少了点什么,所以再这仍然将其列举出来。单向链表单向链表是链表中的一种,它的特点是只有一个指向下一个节点的指针域,对单向链表的访问需要从头部开始,根据指针域依次访问下一个节点,单向链表的结构如下图所示单向链表的创建单向链表的结构只需要一个数据域与指针域,这个数据域可以是一个结构体,也可以是多个基本数据类型;指针域是一个指向节点类型的指针,简单的定义如下:typedef struct _LIST_NODE { int nVal; struct _LIST_NODE *pNext; }LIST_NODE, *LPLIST_NODE;创建链表可以采用头插法或者尾插法来初始化一个有多个节点的链表头插法的示意图如下:它的过程就像示意图中展现的,首先使用新节点p的next指针指向当前的头节点把新节点加入到链表头,然后变更链表头指针,这样就在头部插入了一个节点,用代码来展示就是p->next = head; head = p;我们使用一个函数来封装就是LPLIST_NODE CreateListHead() { LPLIST_NODE pHead = NULL; while (TRUE) { LPLIST_NODE p = (LPLIST_NODE)malloc(sizeof(LIST_NODE)); if (NULL == p) { break; } memset(p, 0x00, sizeof(LIST_NODE)); printf("请输入节点值(为0时将退出创建节点):"); scanf_s("%d", &p->nVal); //这里不需要对链表为空单独讨论 //当链表为空时pHead 的值为NULL, 这两句代码就变为 //p->pNext = NULL; //pHead = p; p->pNext = pHead; pHead = p; if (p->nVal == 0) { break; } } return pHead; }采用尾插法的话,首先得获得链表的尾部 pTail, 然后使尾节点的next指针指向新节点,然后更新尾节点,用代码来表示就是pTail->next = p; pTail = p;下面的函数是采用尾插法来构建链表的例子//这个函数多定义了一个变量用来保存 // 可以不需要这个变量,这样在插入之前需要遍历一遍链表,以便找到尾节点 // 但是每次插入之前都需要遍历一遍,没有定义一个变量保存尾节点这种方式来的高效 LPLIST_NODE CreateListTail() { LPLIST_NODE pHead = NULL; LPLIST_NODE pTail = pHead; while (NULL != pTail && NULL != pTail->pNext) { pTail = pTail->pNext; } while (TRUE) { LPLIST_NODE p = (LPLIST_NODE)malloc(sizeof(LIST_NODE)); if (NULL == p) { break; } memset(p, 0x00, sizeof(LIST_NODE)); printf("请输入节点值(为0时将退出创建节点):"); scanf_s("%d", &p->nVal); //由于这种方法需要对尾节点的next域赋值,所以需要考虑链表为空的情况 if (NULL == pTail) { pHead = p; pTail = pHead; }else { pTail->pNext = p; pTail = p; } if (p->nVal == 0) { break; } } return pHead; }链表的遍历链表的每个节点在内存中不是连续的,所以它不能像数组那样根据下标来访问(当然可以利用C++中的运算符重载来实现使用下标访问),链表中的每一个节点都保存了下一个节点的地址,所以我们根据每个节点指向的下一个节点来依次访问每个节点,访问的代码如下:void TraverseList(LPLIST_NODE pHead) { while (NULL != pHead) { printf("%d\n", pHead->nVal); pHead = pHead->pNext; } }链表的删除链表的每个节点都是在堆上分配的,在不再使用的时候需要手工清除每个节点。清除时需要使用遍历的方法,一个个的删除,只是需要在遍历的指针移动到下一个节点前保存当前节点,以便能够删除当前节点,删除的函数如下void DestroyList(LPLIST_NODE pHead) { LPLIST_NODE pTmp = pHead; while (NULL != pTmp) { pTmp = pHead->pNext; delete pHead; pHead = pTmp; } }删除单个节点如上图所示,假设我们要删除q节点,那么首先需要遍历找到q的上一个节点p,将p的next指针指向q的下一个节点,也就是赋值为q的next指针的值,用代码表示就是p->next = q->next;删除节点的函数如下:void DeleteNode(LPLIST_NODE* ppHead, int nValue) { if (NULL == ppHead || NULL == *ppHead) { return; } LPLIST_NODE p, q; p = *ppHead; while (NULL != p) { if (nValue == p->nVal) { if (*ppHead == p) { *ppHead = p->pNext; free(p); }else { q->pNext = p->pNext; free(p); } p = NULL; q = NULL; break; } q = p; p = p->pNext; } }在上述代码中首先来遍历链表,找到要删除的节点p和它的上一个节点q,由于头节点没有上一个节点,所以需要特别判断一下需要删除的是否为头节点,如果为头结点,则直接将头指针指向它的下一个节点,然后删除头结点即可,如果不是则采用之前的方法来删除。任意位置插入节点如上图所示,如果需要在q节点之后插入p节点的话,需要两步,将q的next节点指向q,然后将q指向之前p的下一个节点,这个时候需要注意一下顺序,如果我们先执行q->next = p 的话,那么之前q的下一个节点的地址就被覆盖掉了,这个时候后面的节点都丢掉了,所以这里我们要先执行p->next = q->next 这条语句,然后在执行q->next = p下面是一个创建有序链表的例子,这个例子演示了在任意位置插入节点LPLIST_NODE CreateSortedList() { LPLIST_NODE pHead = NULL; while (TRUE) { LPLIST_NODE p = (LPLIST_NODE)malloc(sizeof(LIST_NODE)); if (NULL == p) { break; } memset(p, 0x00, sizeof(LIST_NODE)); printf("请输入节点值(为0时将退出创建节点):"); scanf_s("%d", &p->nVal); if (NULL == pHead) { pHead = p; }else { if (pHead->nVal > p->nVal) { p->pNext = pHead; pHead = p; }else { LPLIST_NODE q = pHead; LPLIST_NODE r = q; q = q->pNext; while (NULL != q && q->nVal < p->nVal) { r = q; q = q->pNext; } p->pNext = r->pNext; r->pNext = p; } } if (p->nVal == 0) { break; } } return pHead; }当确定新节点的值之后,首先遍历链表,直到找到比新节点中数值大的节点,那么这个新节点就是需要插入到该节点之前。在遍历的时候使用r来保存之前的节点。这里需要注意这些情况:链表为空:这种情况下,直接让头指针指向当前节点如果头节点本身就是大于新节点的值,这种情况下采用头插法,将新节点插入到头部如果链表中未找到比新节点的值更大的值,这种情况下直接采用尾插发在链表中找到比新节点值更大的节点,这种情况下,在链表中插入但是在代码中并没有考虑到尾部插入的情况,由于在尾部插入时,r等于尾节点,r->pNext 的值为NULL, 所以 p->pNext = r->pNext;r->pNext = p; 可以看成 p->pNext = NULL; r->pNext = p; 也就是将p的next指针指向空,让其作为尾节点,将之前的尾节点的next指针指向新节点。循环链表循环链表是建立在单向链表的基础之上的,循环链表的尾节点并不指向空,而是指向其他的节点,可以是头结点,可以是自身,也可以是链表中的其他节点,为了方便操作,一般将循环链表的尾节点的next指针指向头节点,它的操作与单链表的操作类似,只需要将之前判断尾节点的条件变为 pTail->pNext == pHead 即可。这里就不再详细分析每种操作了,直接给出代码LPLIST_NODE CreateLoopList() { LPLIST_NODE pHead = NULL; LPLIST_NODE pTail = pHead; while(1) { LPLIST_NODE p = (LPLIST_NODE)malloc(sizeof(LIST_NODE)); if (NULL == p) { break; } memset(p, 0x00, sizeof(LIST_NODE)); printf("请输入一个值:"); scanf_s("%d", &p->nVal); if (NULL == pHead) { pHead = p; p->pNext = pHead; pTail = pHead; }else { pTail->pNext = p; p->pNext = pHead; pTail = p; } if (0 == p->nVal) { break; } } return pHead; } void TraverseLoopList(LPLIST_NODE pHead) { LPLIST_NODE pTmp = pHead; if (NULL == pTmp) { return; } do { printf("%d, ", pTmp->nVal); pTmp = pTmp->pNext; } while (pTmp != pHead); } void DestroyLoopList(LPLIST_NODE pHead) { LPLIST_NODE pTmp = pHead; LPLIST_NODE pDestroy = pTmp; if (NULL == pTmp) { return; } do { pTmp = pDestroy->pNext; free(pDestroy); pDestroy = pTmp; }while (pHead != pTmp); }判断链表是否为循环链表在上面说过,循环链表的尾指针不一定指向头节点,它可以指向任何节点,那么该怎么判断一个节点是否为循环链表呢?既然它可以指向任意的节点,那么肯定是找不到尾节点的,而且堆内存的分配是随机的,我们也不可能按照指针变量的大小来判断哪个节点在前哪个在后。回想一下在学校跑一千米的时候是不是回出现这样的情况,跑的块的会领先跑的慢的一周?根据这种情形我们可以考虑使用这样一种办法:定义两个指针,一个一次走两步也是就是p = p->next->next, 一个慢指针一次走一步,也就是q = q->next,如果是循环链表,那么快指针在某个时候一定会领先慢指针一周,也就是达到 p == q 这个条件,否则就是非循环链表。根据这个思路,可以考虑写下如下代码:bool IsLoopList(LPLIST_NODE pHead) { if (NULL == pHead) { return false; } LPLIST_NODE p = pHead; LPLIST_NODE q = pHead->pNext; while (NULL != p && NULL != q && NULL != q->pNext && p != q) { p = p->pNext; q = q->pNext->pNext; } if (q == NULL || NULL == p || NULL == q->pNext) { return false; } return true; }双向链表之前在插入或者删除的时候,需要定义两个指针变量,让其中一个一直更在另一个的后面,单向链表有一个很大的问题,不能很方便的找到它的上一个节点,为了解决这一个问题,提出了双向链表,双向链表与单向相比,多了一个指针域,用来指向它的上一个节点,也就是如下图所示:双向链表的操作与单向链表的类似,只是多了一个指向前一个节点的指针域,它要考虑的情况与单向链表相似删除节点删除节点的示意图如下:假设删除的节点p,那么首先根据p的pre指针域,找到它的上一个节点q,采用与单向链表类似的操作:q->next = p->next; p->next->pre = q;下面是删除节点的例子:void DeleteDNode(LPDLIST_NODE* ppHead, int nValue) { if (NULL == ppHead || NULL == *ppHead) { return; } LPDLIST_NODE p = *ppHead; while (NULL != p && p->nVal != nValue) { p = p->pNext; } if (NULL == p) { return; } if (*ppHead == p) { *ppHead = (*ppHead)->pNext; p->pPre = NULL; free(p); } else if (p->pNext == NULL) { p->pPre->pNext = NULL; free(p); }else { p->pPre->pNext = p->pNext; p->pNext->pPre = p->pPre; } }插入节点插入节点的示意图如下:假设新节点为p,插入的位置为q,则插入操作可以进行如下操作p->next = q->next; p->pre = q; q->next->pre = p; q->next = p;也是一样要考虑不能覆盖q的next指针域否则可能存在找不到原来链表中q的下一个节点的情况。所以这里先对p的next指针域进行操作下面也是采用创建有序列表的例子LPDLIST_NODE CreateSortedDList() { LPDLIST_NODE pHead = NULL; while (1) { LPDLIST_NODE pNode = (LPDLIST_NODE)malloc(sizeof(DLIST_NODE)); if (NULL == pNode) { return pHead; } memset(pNode, 0x00, sizeof(DLIST_NODE)); printf("请输入一个整数:"); scanf_s("%d", &pNode->nVal); if(NULL == pHead) { pHead = pNode; }else { LPDLIST_NODE q = pHead; LPDLIST_NODE r = q; while (NULL != q && q->nVal < pNode->nVal) { r = q; q = q->pNext; } if (q == pHead) { pNode->pNext = pHead; pHead->pPre = pNode; pHead = pNode; }else if (NULL == q) { r->pNext = pNode; pNode->pPre = r; }else { pNode->pPre = r; pNode->pNext = q; r->pNext = pNode; q->pPre = pNode; } } LPDLIST_NODE q = pHead; LPDLIST_NODE r = q; if (0 == pNode->nVal) { break; } } return pHead; }链表还有一种是双向循环链表,对于这种链表主要是在双向链表的基础上,将头结点的pre指针指向某个节点,将尾节点的next节点指向某个节点,而且这两个指针可以指向同一个节点也可以指向不同的节点,一般在使用中都是head的pre节点指向尾节点,而tail的next节点指向头节点。这里就不再详细说明,这些链表只要掌握其中一种,剩下的很好掌握的。 -
 算法与数据结构(一):时间复杂度与空间复杂度 最近突然萌生了一个想法,好好系统的学习一下算法与数据结构然后产生一系列的文章来回顾与总结学到的东西,这部分我想从最简单的部分一一介绍总结,包括一些很基础的内容为什么要学习数据结构与算法以前在学校的时候就知道 程序 = 算法 + 数据结构,程序的作用是用来处理与解决现实问题,而在描述与解决现实问题时不可避免的会涉及到数据,如何将这些数据有效的组织起来并利用一定的方法来运算与处理应该算是程序的核心问题。当然如果仅仅将编程作为谋生的手段,确实不用太关心这部分,现实中很多语言和库都封装了这些东西,需要的时候直接用即可,不懂算法与数据结构并不会对编程产生什么影响,在实际工作中可能并没有机会自己实现一个链表、队列等等。但是如果真正热爱这一行,希望能更上一层楼的,算法与数据结构必定是绕不开的一环。学习数据结构并不是为了要在工作中自己实现它,而是:了解使用算法解决问题的一些思想,能够让你知道如何更好地优化自己的代码了解更多的数据结构与算法的知识,能在编程中更加游刃有余,能更好的解决实际问题程序的性能瓶颈往往都跟算法和数据结构有关系, 好的算法能更多的提升程序的性能当我们面对一个完全未知的问题时,了解更多的算法知识能够多出一些尝试为了能够在面试中脱颖而出当时在学校学习的时候我是被各种系统程序以及各种漂亮的Web程序给吸引了,认为算法这种东西永远都在处理平时根本碰不上的问题,有时间浪费在这些虚无缥缈的东西上还不如学学怎么做一个应用,写一个网站出来。那个时候基本放弃了对这方面的学习。后来在工作中经常出现网上对你所面临的问题没有明确的结局方案,需要在现有的方案上做修改,这个时候就束手无策了。使用了某种算法解决了问题,但是效率不高,遇到大规模访问时容易出错崩溃,这个时候还是没辙。还有就是在网上看别人的开源代码时需要花额外的精力来研究老外的某个写法,其实如果懂点算法的知识,可能并不需要这些额外的时间开销。由于有了这些精力,我想在新年开始的这段时间里研究一下数据结构与算法的相关内容,提升一下自己的基本功。时间复杂度有了前面说的一些经历,下面就进入正题了:算法的时间复杂度与空间复杂度;时间复杂度与空间复杂度是评价一个算法好话的一个常用标准。时间复杂度是以程序代码中基本语句执行次数作为衡量标准。换句话说时间复杂度是用这个算法需要执行代码量来评价的。假设一个问题的规模为n,常见的比如说有n个数据需要进行处理,如果算法是类似这样的:for(int i = 0; i < n; i++) { //do some thing setup1(); for(int j = 0; j < n; j++) { //do something setup2(); } }假设setup1和setup2 函数执行了j、k次运算 那么我们来计算一下这个算法总共执行了多少次:首先在内层循环中循环了n次,那么setup2函数执行了nci,这个时候有 k * n, 外层循环也是执行了n次,所以这个算法总共执行了 n * (j + n * k) = n^2 + n(k + j), 这样得到事件复杂度为 T(n) = n^2 + n(k + j) 由于k j都是常数,所以计算这个时间复杂度又可以写作 T(n) = n^2 + nt, 对于这个表达式取自高次幂 得到这个算法的时间复杂度为 T(n) = n^2从上面的计算来看,计算事件复杂度就是计算它需要执行基本代码执行多少次,然后将得到的表达式取最高次幂并去掉系数。常见的时间复杂度有O(1)、O(logn)、O(n)、O(nlogn)、O(n^2)、O(n^k)、O(n!)、O(2^n)从效率上看,它们是依次降低的。一般来说算法最多达到O(n^2), 如果比O(n^2)高,这个时候就需要好好考虑一下优化算法了。一般常见的算法时间复杂度如下:每层循环,时间复杂度都需要在原来的基础之上乘以n没有循环的时间复杂度一般为常数二分法时间复杂度为logn空间复杂度空间复杂度是指算法占用内存空间的值,需要注意的是,这个内存占用主要是在算法内部动态分配了内存,算法函数中的临时变量储存在栈空间,算法执行完成后会回收,一般不考虑局部变量占用的内存。同时静态变量,全局变量都不考虑进来在算法中值考虑在函数中分配的内存以及递归调用时栈空间的占用内存。计算算法的空间复杂度并不复杂,因此这里就不给例子了。算法的空间复杂度应该控制在O(1),也就是尽量不要在算法内部分配内存,少用递归。
算法与数据结构(一):时间复杂度与空间复杂度 最近突然萌生了一个想法,好好系统的学习一下算法与数据结构然后产生一系列的文章来回顾与总结学到的东西,这部分我想从最简单的部分一一介绍总结,包括一些很基础的内容为什么要学习数据结构与算法以前在学校的时候就知道 程序 = 算法 + 数据结构,程序的作用是用来处理与解决现实问题,而在描述与解决现实问题时不可避免的会涉及到数据,如何将这些数据有效的组织起来并利用一定的方法来运算与处理应该算是程序的核心问题。当然如果仅仅将编程作为谋生的手段,确实不用太关心这部分,现实中很多语言和库都封装了这些东西,需要的时候直接用即可,不懂算法与数据结构并不会对编程产生什么影响,在实际工作中可能并没有机会自己实现一个链表、队列等等。但是如果真正热爱这一行,希望能更上一层楼的,算法与数据结构必定是绕不开的一环。学习数据结构并不是为了要在工作中自己实现它,而是:了解使用算法解决问题的一些思想,能够让你知道如何更好地优化自己的代码了解更多的数据结构与算法的知识,能在编程中更加游刃有余,能更好的解决实际问题程序的性能瓶颈往往都跟算法和数据结构有关系, 好的算法能更多的提升程序的性能当我们面对一个完全未知的问题时,了解更多的算法知识能够多出一些尝试为了能够在面试中脱颖而出当时在学校学习的时候我是被各种系统程序以及各种漂亮的Web程序给吸引了,认为算法这种东西永远都在处理平时根本碰不上的问题,有时间浪费在这些虚无缥缈的东西上还不如学学怎么做一个应用,写一个网站出来。那个时候基本放弃了对这方面的学习。后来在工作中经常出现网上对你所面临的问题没有明确的结局方案,需要在现有的方案上做修改,这个时候就束手无策了。使用了某种算法解决了问题,但是效率不高,遇到大规模访问时容易出错崩溃,这个时候还是没辙。还有就是在网上看别人的开源代码时需要花额外的精力来研究老外的某个写法,其实如果懂点算法的知识,可能并不需要这些额外的时间开销。由于有了这些精力,我想在新年开始的这段时间里研究一下数据结构与算法的相关内容,提升一下自己的基本功。时间复杂度有了前面说的一些经历,下面就进入正题了:算法的时间复杂度与空间复杂度;时间复杂度与空间复杂度是评价一个算法好话的一个常用标准。时间复杂度是以程序代码中基本语句执行次数作为衡量标准。换句话说时间复杂度是用这个算法需要执行代码量来评价的。假设一个问题的规模为n,常见的比如说有n个数据需要进行处理,如果算法是类似这样的:for(int i = 0; i < n; i++) { //do some thing setup1(); for(int j = 0; j < n; j++) { //do something setup2(); } }假设setup1和setup2 函数执行了j、k次运算 那么我们来计算一下这个算法总共执行了多少次:首先在内层循环中循环了n次,那么setup2函数执行了nci,这个时候有 k * n, 外层循环也是执行了n次,所以这个算法总共执行了 n * (j + n * k) = n^2 + n(k + j), 这样得到事件复杂度为 T(n) = n^2 + n(k + j) 由于k j都是常数,所以计算这个时间复杂度又可以写作 T(n) = n^2 + nt, 对于这个表达式取自高次幂 得到这个算法的时间复杂度为 T(n) = n^2从上面的计算来看,计算事件复杂度就是计算它需要执行基本代码执行多少次,然后将得到的表达式取最高次幂并去掉系数。常见的时间复杂度有O(1)、O(logn)、O(n)、O(nlogn)、O(n^2)、O(n^k)、O(n!)、O(2^n)从效率上看,它们是依次降低的。一般来说算法最多达到O(n^2), 如果比O(n^2)高,这个时候就需要好好考虑一下优化算法了。一般常见的算法时间复杂度如下:每层循环,时间复杂度都需要在原来的基础之上乘以n没有循环的时间复杂度一般为常数二分法时间复杂度为logn空间复杂度空间复杂度是指算法占用内存空间的值,需要注意的是,这个内存占用主要是在算法内部动态分配了内存,算法函数中的临时变量储存在栈空间,算法执行完成后会回收,一般不考虑局部变量占用的内存。同时静态变量,全局变量都不考虑进来在算法中值考虑在函数中分配的内存以及递归调用时栈空间的占用内存。计算算法的空间复杂度并不复杂,因此这里就不给例子了。算法的空间复杂度应该控制在O(1),也就是尽量不要在算法内部分配内存,少用递归。