搜索到
149
篇与
的结果
-
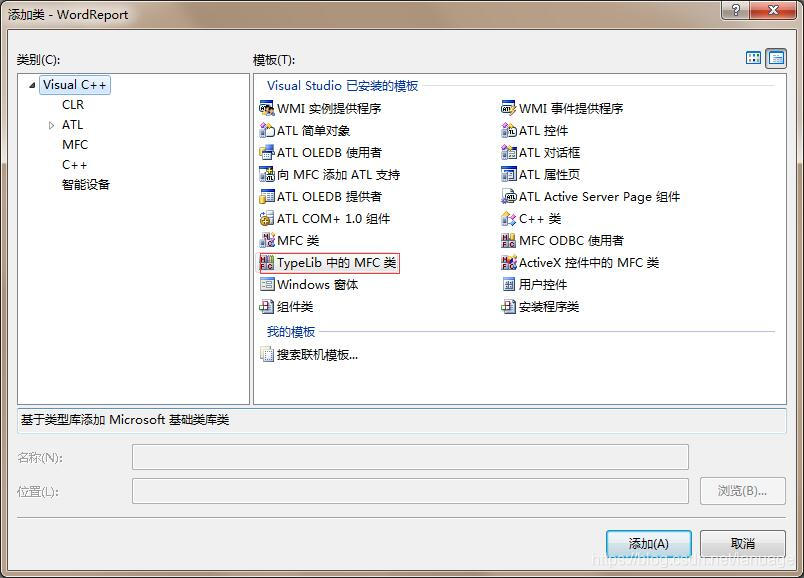
 VC+++ 操作word 最近完成了一个使用VC++ 操作word生成扫描报告的功能,在这里将过程记录下来,开发环境为visual studio 2008导入接口首先在创建的MFC项目中引入word相关组件右键点击 项目 --> 添加 --> 新类,在弹出的对话框中选择Typelib中的MFC类。然后在弹出的对话框中选择文件,从文件中导入MSWORD.OLB组件。这个文件的路径一般在C:\Program Files (x86)\Microsoft Office\Office14 中,注意:最后一层可能不一定是Office14,这个看机器中安装的office 版本。选择之后会要求我们决定导入那些接口,为了方便我们导入所有接口。导入之后可以看到项目中省成本了很多代码文件,这些就是系统生成的操作Word的相关类。这里编译可能会报错,error C2786: “BOOL (HDC,int,int,int,int)”: __uuidof 的操作数无效解决方法:修改对应头文件#import "C:\\Program Files\\Microsoft Office\\Office14\\MSWORD.OLB" no_namespace为:#import "C:\\Program Files\\Microsoft Office\\Office14\\MSWORD.OLB" no_namespace raw_interfaces_only \ rename("FindText","_FindText") \ rename("Rectangle","_Rectangle") \ rename("ExitWindows","_ExitWindows")再次编译,错误消失常见接口介绍要了解一些常见的类,我们首先需要明白这些接口的层次结构:Application(WORD 为例,只列出一部分) Documents(所有的文档) Document(一个文档) ...... Templates(所有模板) Template(一个模板) ...... Windows(所有窗口) Window Selection View Selection(编辑对象) Font Style Range这些组件其实是采用远程调用的方式调用word进程来完成相关操作。Application:相当于一个word进程,每次操作之前都需要一个application对象,这个对象用于创建一个word进程。Documents:相当于word中打开的所有文档,如果用过word编辑多个文件,那么这个概念应该很好理解Templates:是一个模板对象,至于word模板,不了解的请自行百度Windows:word进程中的窗口Selection:编辑对象。也就是我们要写入word文档中的内容。一般包括文本、样式、图形等等对象。回忆一下我们手动编写word的情景,其实使用这些接口是很简单的。我们在使用word编辑的时候首先会打开word程序,这里对应在代码里面就是创建一个Application对象。然后我们会用word程序打开一个文档或者新建一个文档。这里对应着创建Documents对象并从中引用一个Document对象表示一个具体的文档。当然这个Document对象可以是新建的也可以是打开一个现有的。接着就是进行相关操作了,比如插入图片、插入表格、编写段落文本等等了。这些都对应着创建类似于Font、Style、TypeText对象,然后将这些对象进行添加的操作了。说了这么多。这些接口这么多,我怎么知道哪个接口对应哪个对象呢,而且这些参数怎么传递呢?其实这个问题很好解决。我们可以手工进行相关操作,然后用宏记录下来,最后我们再将宏中的VB代码转化为VC代码即可。相关操作为了方便在项目中使用,这里创建一个类用于封装Word的相关操作class CCreateWordReport { private: CApplication m_wdApp; CDocuments m_wdDocs; CDocument0 m_wdDoc; CSelection m_wdSel; CRange m_wdRange; CnlineShapes m_wdInlineShapes; CnlineShape m_wdInlineShape; public: CCreateWordReport(); virtual ~CCreateWordReport(); public: //操作 //**********************创建新文档******************************************* BOOL CreateApp(); //创建一个新的WORD应用程序 BOOL CreateDocuments(); //创建一个新的Word文档集合 BOOL CreateDocument(); //创建一个新的Word文档 BOOL Create(); //创建新的WORD应用程序并创建一个新的文档 void ShowApp(); //显示WORD文档 void HideApp(); //隐藏word文档 //**********************打开文档********************************************* BOOL OpenDocument(CString fileName);//打开已经存在的文档。 BOOL Open(CString fileName); //创建新的WORD应用程序并打开一个已经存在的文档。 BOOL SetActiveDocument(short i); //设置当前激活的文档。 //**********************保存文档********************************************* BOOL SaveDocument(); //文档是以打开形式,保存。 BOOL SaveDocumentAs(CString fileName);//文档以创建形式,保存。 BOOL CloseDocument(); void CloseApp(); //**********************文本书写操作***************************************** void WriteText(CString szText); //当前光标处写文本 void WriteNewLineText(CString szText, int nLineCount = 1); //换N行写字 void WriteEndLine(CString szText); //文档结尾处写文本 void WholeStory(); //全选文档内容 void Copy(); //复制文本内容到剪贴板 void InsertFile(CString fileName); //将本地的文件全部内容写入到当前文档的光标处。 void InsertTable(int nRow, int nColumn, CTable0& wdTable); //**********************图片插入操作***************************************** void InsertShapes(CString fileName);//在当前光标的位置插入图片 //**********************超链接插入操作***************************************** void InsertHyperlink(CString fileLink);//超级链接地址,可以是相对路径。 //***********************表格操作表格操作********************************** BOOL InsertTableToMarkBook(const CString csMarkName, int nRow, int nColumn, CTable0& wdTable); //表格行数与列数 BOOL WriteDataToTable(CTable0& wdTable, int nRow, int nColumn, const CString &csData); //往表格中写入输入 };BOOL CCreateWordReport::CreateApp() { if (FALSE == m_wdApp.CreateDispatch("word.application")) { AfxMessageBox("Application创建失败,请确保安装了word 2000或以上版本!", MB_OK|MB_ICONWARNING); return FALSE; } return TRUE; } BOOL CCreateWordReport::CreateDocuments() { if (FALSE == CreateApp()) { return FALSE; } m_wdDocs = m_wdApp.get_Documents(); if (!m_wdDocs.m_lpDispatch) { AfxMessageBox("Documents创建失败!", MB_OK|MB_ICONWARNING); return FALSE; } return TRUE; } BOOL CCreateWordReport::CreateDocument() { if (!m_wdDocs.m_lpDispatch) { AfxMessageBox("Documents为空!", MB_OK|MB_ICONWARNING); return FALSE; } COleVariant varTrue(short(1),VT_BOOL),vOptional((long)DISP_E_PARAMNOTFOUND, VT_ERROR); CComVariant Template(_T("")); //没有使用WORD的文档模板 CComVariant NewTemplate(false),DocumentType(0),Visible; m_wdDocs.Add(&Template,&NewTemplate,&DocumentType,&Visible); //得到document变量 m_wdDoc = m_wdApp.get_ActiveDocument(); if (!m_wdDoc.m_lpDispatch) { AfxMessageBox("Document获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } //得到selection变量 m_wdSel = m_wdApp.get_Selection(); if (!m_wdSel.m_lpDispatch) { AfxMessageBox("Select获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } //得到Range变量 m_wdRange = m_wdDoc.Range(vOptional,vOptional); if(!m_wdRange.m_lpDispatch) { AfxMessageBox("Range获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } return TRUE; } BOOL CCreateWordReport::Create() { if (FALSE == CreateDocuments()) { return FALSE; } return CreateDocument(); } BOOL CCreateWordReport::OpenDocument(CString fileName) { if (!m_wdDocs.m_lpDispatch) { AfxMessageBox("Documents为空!", MB_OK|MB_ICONWARNING); return FALSE; } COleVariant vTrue((short)TRUE), vFalse((short)FALSE), vOptional((long)DISP_E_PARAMNOTFOUND, VT_ERROR), vZ((short)0); COleVariant vFileName(_T(fileName)); //得到document变量 m_wdDoc = m_wdDocs.Open( vFileName, // FileName vTrue, // Confirm Conversion. vFalse, // ReadOnly. vFalse, // AddToRecentFiles. vOptional, // PasswordDocument. vOptional, // PasswordTemplate. vOptional, // Revert. vOptional, // WritePasswordDocument. vOptional, // WritePasswordTemplate. vOptional, // Format. // Last argument for Word 97 vOptional, // Encoding // New for Word 2000/2002 vOptional, // Visible /*如下4个是word2003需要的参数。本版本是word2000。*/ vOptional, // OpenAndRepair vZ, // DocumentDirection wdDocumentDirection LeftToRight vOptional, // NoEncodingDialog vOptional ); if (!m_wdDoc.m_lpDispatch) { AfxMessageBox("Document获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } //得到selection变量 m_wdSel = m_wdApp.get_Selection(); if (!m_wdSel.m_lpDispatch) { AfxMessageBox("Select获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } //得到全部DOC的Range变量 m_wdRange = m_wdDoc.Range(vOptional,vOptional); if(!m_wdRange.m_lpDispatch) { AfxMessageBox("Range获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } return TRUE; } BOOL CCreateWordReport::Open(CString fileName) { if (FALSE == CreateDocuments()) { return FALSE; } return OpenDocument(fileName); } BOOL CCreateWordReport::SetActiveDocument(short i) { COleVariant vIndex(_T(i)),vOptional((long)DISP_E_PARAMNOTFOUND, VT_ERROR); m_wdDoc.AttachDispatch(m_wdDocs.Item(vIndex)); m_wdDoc.Activate(); if (!m_wdDoc.m_lpDispatch) { AfxMessageBox("Document获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } //得到selection变量 m_wdSel = m_wdApp.get_Selection(); if (!m_wdSel.m_lpDispatch) { AfxMessageBox("Select获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } //得到全部DOC的Range变量 m_wdRange = m_wdDoc.Range(vOptional,vOptional); if(!m_wdRange.m_lpDispatch) { AfxMessageBox("Range获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } // HideApp(); return TRUE; } BOOL CCreateWordReport::SaveDocument() { if (!m_wdDoc.m_lpDispatch) { AfxMessageBox("Document获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } m_wdDoc.Save(); return TRUE; } BOOL CCreateWordReport::SaveDocumentAs(CString fileName) { if (!m_wdDoc.m_lpDispatch) { AfxMessageBox("Document获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } COleVariant covOptional((long)DISP_E_PARAMNOTFOUND,VT_ERROR); COleVariant varZero((short)0); COleVariant varTrue(short(1),VT_BOOL); COleVariant varFalse(short(0),VT_BOOL); COleVariant vFileName(_T(fileName)); m_wdDoc.SaveAs( vFileName, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional ); return TRUE; } BOOL CCreateWordReport::CloseDocument() { COleVariant vTrue((short)TRUE), vFalse((short)FALSE), vOptional((long)DISP_E_PARAMNOTFOUND, VT_ERROR); m_wdDoc.Close(vFalse, // SaveChanges. vTrue, // OriginalFormat. vFalse // RouteDocument. ); m_wdDoc.AttachDispatch(m_wdApp.get_ActiveDocument()); if (!m_wdDoc.m_lpDispatch) { AfxMessageBox("Document获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } //得到selection变量 m_wdSel = m_wdApp.get_Selection(); if (!m_wdSel.m_lpDispatch) { AfxMessageBox("Select获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } //得到全部DOC的Range变量 m_wdRange = m_wdDoc.Range(vOptional,vOptional); if(!m_wdRange.m_lpDispatch) { AfxMessageBox("Range获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } return TRUE; } void CCreateWordReport::CloseApp() { COleVariant vTrue((short)TRUE), vFalse((short)FALSE), vOptional((long)DISP_E_PARAMNOTFOUND, VT_ERROR); m_wdDoc.Save(); m_wdApp.Quit(vFalse, // SaveChanges. vTrue, // OriginalFormat. vFalse // RouteDocument. ); //释放内存申请资源 m_wdInlineShape.ReleaseDispatch(); m_wdInlineShapes.ReleaseDispatch(); //m_wdTb.ReleaseDispatch(); m_wdRange.ReleaseDispatch(); m_wdSel.ReleaseDispatch(); //m_wdFt.ReleaseDispatch(); m_wdDoc.ReleaseDispatch(); m_wdDocs.ReleaseDispatch(); m_wdApp.ReleaseDispatch(); } void CCreateWordReport::WriteText(CString szText) { m_wdSel.TypeText(szText); } void CCreateWordReport::WriteNewLineText(CString szText, int nLineCount /* = 1 */) { int i; if (nLineCount <= 0) { nLineCount = 0; } for (i = 0; i < nLineCount; i++) { m_wdSel.TypeParagraph(); } WriteText(szText); } void CCreateWordReport::WriteEndLine(CString szText) { m_wdRange.InsertAfter(szText); } void CCreateWordReport::WholeStory() { m_wdRange.WholeStory(); } void CCreateWordReport::Copy() { m_wdRange.CopyAsPicture(); } void CCreateWordReport::InsertFile(CString fileName) { COleVariant vFileName(fileName), vTrue((short)TRUE), vFalse((short)FALSE), vOptional((long)DISP_E_PARAMNOTFOUND, VT_ERROR), vNull(_T("")); /* void InsertFile(LPCTSTR FileName, VARIANT* Range, VARIANT* ConfirmConversions, VARIANT* Link, VARIANT* Attachment); */ m_wdSel.InsertFile( fileName, vNull, vFalse, vFalse, vFalse ); } void CCreateWordReport::InsertShapes(CString fileName) { COleVariant vTrue((short)TRUE), vFalse((short)FALSE), vOptional((long)DISP_E_PARAMNOTFOUND, VT_ERROR); m_wdInlineShapes=m_wdSel.get_InlineShapes(); m_wdInlineShape=m_wdInlineShapes.AddPicture(fileName,vFalse,vTrue,vOptional); } void CCreateWordReport::InsertHyperlink(CString fileLink) { COleVariant vAddress(_T(fileLink)),vSubAddress(_T("")); CRange aRange = m_wdSel.get_Range(); CHyperlinks vHyperlinks(aRange.get_Hyperlinks()); vHyperlinks.Add( aRange, //Object,必需。转换为超链接的文本或图形。 vAddress, //Variant 类型,可选。指定的链接的地址。此地址可以是电子邮件地址、Internet 地址或文件名。请注意,Microsoft Word 不检查该地址的正确性。 vSubAddress, //Variant 类型,可选。目标文件内的位置名,如书签、已命名的区域或幻灯片编号。 vAddress, //Variant 类型,可选。当鼠标指针放在指定的超链接上时显示的可用作“屏幕提示”的文本。默认值为 Address。 vAddress, //Variant 类型,可选。指定的超链接的显示文本。此参数的值将取代由 Anchor 指定的文本或图形。 vSubAddress //Variant 类型,可选。要在其中打开指定的超链接的框架或窗口的名字。 ); aRange.ReleaseDispatch(); vHyperlinks.ReleaseDispatch(); }这样我们就封装好了一些基本的操作,其实这些操作都是我自己根据网上的资料以及VB宏转化而来得到的代码。特殊操作在这里主要介绍一些比较骚的操作,这也是这篇文章主要有用的内容,前面基本操作网上都有源代码直接拿来用就OK了,这里的骚操作是我在项目中使用的主要操作,应该有应用价值。先请各位仔细想想,如果我们要根据前面的代码,从0开始完全用代码生成一个完整的报表是不是很累,而且一般报表都会包含一些通用的废话,这些话基本不会变化。如果将这些写到代码里面,如果后面这些话变了,我们就要修改并重新编译,是不是很麻烦。所以这里介绍的第一个操作就是利用模板和书签在合适的位置插入内容。书签的使用首先我们在Word中的适当位置创建一个标签,至于如何创建标签,请自行百度。然后在代码中的思路就是在文档中查找我们的标签,再获取光标的位置,最后就是在该位置处添加相应的内容了,这里我们举一个在光标位置插入文本的例子:void CCreateWordReport::WriteTextToBookMark(const CString& csMarkName, const CString& szText) { CBookmarks bks = m_wdDoc.get_Bookmarks(); //获取文档中的所有书签 CBookmark0 bk; COleVariant bk_name(csMarkName); bk = bks.Item(&bk_name); //查询对应名称的书签 CRange hRange = bk.get_Range(); //获取书签位置 if (hRange != NULL) { hRange.put_Text(szText); //在该位置处插入文本 } //最后不要忘记清理相关资源 hRange.ReleaseDispatch(); bk.ReleaseDispatch(); bks.ReleaseDispatch(); }表格的使用在word报表中表格应该是一个重头戏,表格中常用的接口如下:CTables0: 表格集合CTable0: 某个具体的表格,一般通过CTables来创建CTableCColumn: 表格列对象CRow:表格行对象CCel:表格单元格对象创建表格一般的操作如下:void CCreateWordReport::InsertTable(int nRow, int nColumn, CTable0& wdTable) { VARIANT vtDefault; COleVariant vtAuto; vtDefault.vt = VT_INT; vtDefault.intVal = 1; vtAuto.vt = VT_INT; vtAuto.intVal = 0; CTables0 wordtables = m_wdDoc.get_Tables(); wdTable = wordtables.Add(m_wdSel.get_Range(), nRow, nColumn, &vtDefault, &vtAuto); wordtables.ReleaseDispatch(); }往表格中写入内容的操作如下:BOOL CCreateWordReport::WriteDataToTable(CTable0& wdTable, int nRow, int nColumn, const CString &csData) { CCell cell = wdTable.Cell(nRow, nColumn); cell.Select(); //将光标移动到单元格 m_wdSel.TypeText(csData); cell.ReleaseDispatch(); return TRUE; }合并单元格的操作如下:CTable0 wdTable; InsertTable(5, 3, wdTable); //创建一个5行3列的表格 CCell cell = wdTable.Cell(1, 1); //获得第一行第一列的单元格 //设置第二列列宽 CColumns0 columns = wdTable.get_Columns(); CColumn col; col.AttachDispatch(columns.Item(2)); col.SetWidth(40, 1); cell.Merge(wdTable.Cell(5, 1)); //合并单元格,一直合并到第5行的第1列。 cell.SetWidth(30, 1); cell.ReleaseDispatch();合并单元格用的是Merge函数,该函数的参数是一个单元格对象,表示合并结束的单元格。这里合并类似于我们画矩形时提供的左上角坐标和右下角坐标移动光标跳出表格当时由于需要连续的生成多个表格,当时我将前一个表格的数据填完,光标位于最后一个单元格里面,这个时候如果再插入的时候会在这个单元格里面插入表格,这个时候需要我手动向下移动光标,让光标移除到表格外。移动光标的代码如下:m_wdSel.MoveDown(&COleVariant((short)wdLine), &COleVariant((short)1), &COleVariant((short)wdNULL)); 这里wdLine 是word相关接口定义的,表示希望以何种单位来移动,这里我是以行为单位。后面的1表示移动1行。但是我发现在面临换页的时候一次移动根本移动不出来,这个时候我又添加了一行这样的代码移动两行。但是问题又出现了,这一系列表格后面跟着另一个大标题,多移动几次之后可能会造成它移动到大标题的位置,而破坏我原来定义的模板,这个时候该怎么办呢?我采取的办法是,判断当前光标是否在表格中,如果是则移动一行,知道出了表格。这里的代码如下://移动光标,直到跳出表格外 while (TRUE) { m_wdSel.MoveDown(&COleVariant((short)wdLine), &COleVariant((short)1), &COleVariant((short)wdNULL)); m_wdSel.Collapse(&COleVariant((short)wdCollapseStart)); if (!m_wdSel.get_Information((long)wdWithInTable).boolVal) { break; } }样式的使用在使用样式的时候当然也可以用代码来定义,但是我们可以采取另一种方式,我们可以事先在模板文件中创建一系列样式,然后在需要的时候直接定义段落或者文本的样式即可m_wdSel.put_Style(COleVariant("二级标题")); //在当前光标处的样式定义为二级标题样式,这里的二级标题样式是我们在word中事先定义好的 m_wdSel.TypeText(csTitle); //在当前位置输出文本 m_wdSel.TypeParagraph(); //插入段落,这里主要为了换行,这个时候光标也会跟着动 m_wdSel.put_Style(COleVariant("正文")); //定义此处样式为正文样式 m_wdSel.TypeText(csText;插入图表我自己尝试用word生成的图表样式还可以,但是用代码插入的时候,样式就特别丑,这里没有办法,我采用GDI+绘制了一个饼图,然后将图片插入word中。BOOL CCreateWordReport::DrawVulInforPic(const CString& csMarkName, int nVulCnt, int nVulCris, int nHigh, int nMid, int nLow, int nPossible) { CBookmarks bks = m_wdDoc.get_Bookmarks(); COleVariant bk_name(csMarkName); CBookmark0 bk = bks.Item(&bk_name); bk.Select(); CnlineShapes isps = m_wdSel.get_InlineShapes(); COleVariant vFalse((short)FALSE); COleVariant vNull(""); COleVariant vOptional((long)DISP_E_PARAMNOTFOUND,VT_ERROR); //创建一个与桌面环境兼容的内存DC HWND hWnd = GetDesktopWindow(); HDC hDc = GetDC(hWnd); HDC hMemDc = CreateCompatibleDC(hDc); HBITMAP hMemBmp = CreateCompatibleBitmap(hDc, PICTURE_WIDTH + GLOBAL_MARGIN, PICTURE_LENGTH + 2 * GLOBAL_MARGIN + LENGED_BORDER_LENGTH); SelectObject(hMemDc, hMemBmp); //绘制并保存图表 DrawPie(hMemDc, nVulCnt, nVulCris, nHigh, nMid, nLow, nPossible); COleVariant vTrue((short)TRUE); CnlineShape isp=isps.AddPicture("D:\\Program\\WordReport\\WordReport\\test.png",vFalse,vTrue,vOptional); //以图片的方式插入图表 //设置图片的大小 isp.put_Height(141); isp.put_Width(423); bks.ReleaseDispatch(); bk.ReleaseDispatch(); isps.ReleaseDispatch(); isp.ReleaseDispatch(); DeleteObject(hMemDc); DeleteDC(hMemDc); ReleaseDC(hWnd, hDc); return TRUE; }最后,各个接口的参数可以参考下面的链接:.net Word office组件接口文档
VC+++ 操作word 最近完成了一个使用VC++ 操作word生成扫描报告的功能,在这里将过程记录下来,开发环境为visual studio 2008导入接口首先在创建的MFC项目中引入word相关组件右键点击 项目 --> 添加 --> 新类,在弹出的对话框中选择Typelib中的MFC类。然后在弹出的对话框中选择文件,从文件中导入MSWORD.OLB组件。这个文件的路径一般在C:\Program Files (x86)\Microsoft Office\Office14 中,注意:最后一层可能不一定是Office14,这个看机器中安装的office 版本。选择之后会要求我们决定导入那些接口,为了方便我们导入所有接口。导入之后可以看到项目中省成本了很多代码文件,这些就是系统生成的操作Word的相关类。这里编译可能会报错,error C2786: “BOOL (HDC,int,int,int,int)”: __uuidof 的操作数无效解决方法:修改对应头文件#import "C:\\Program Files\\Microsoft Office\\Office14\\MSWORD.OLB" no_namespace为:#import "C:\\Program Files\\Microsoft Office\\Office14\\MSWORD.OLB" no_namespace raw_interfaces_only \ rename("FindText","_FindText") \ rename("Rectangle","_Rectangle") \ rename("ExitWindows","_ExitWindows")再次编译,错误消失常见接口介绍要了解一些常见的类,我们首先需要明白这些接口的层次结构:Application(WORD 为例,只列出一部分) Documents(所有的文档) Document(一个文档) ...... Templates(所有模板) Template(一个模板) ...... Windows(所有窗口) Window Selection View Selection(编辑对象) Font Style Range这些组件其实是采用远程调用的方式调用word进程来完成相关操作。Application:相当于一个word进程,每次操作之前都需要一个application对象,这个对象用于创建一个word进程。Documents:相当于word中打开的所有文档,如果用过word编辑多个文件,那么这个概念应该很好理解Templates:是一个模板对象,至于word模板,不了解的请自行百度Windows:word进程中的窗口Selection:编辑对象。也就是我们要写入word文档中的内容。一般包括文本、样式、图形等等对象。回忆一下我们手动编写word的情景,其实使用这些接口是很简单的。我们在使用word编辑的时候首先会打开word程序,这里对应在代码里面就是创建一个Application对象。然后我们会用word程序打开一个文档或者新建一个文档。这里对应着创建Documents对象并从中引用一个Document对象表示一个具体的文档。当然这个Document对象可以是新建的也可以是打开一个现有的。接着就是进行相关操作了,比如插入图片、插入表格、编写段落文本等等了。这些都对应着创建类似于Font、Style、TypeText对象,然后将这些对象进行添加的操作了。说了这么多。这些接口这么多,我怎么知道哪个接口对应哪个对象呢,而且这些参数怎么传递呢?其实这个问题很好解决。我们可以手工进行相关操作,然后用宏记录下来,最后我们再将宏中的VB代码转化为VC代码即可。相关操作为了方便在项目中使用,这里创建一个类用于封装Word的相关操作class CCreateWordReport { private: CApplication m_wdApp; CDocuments m_wdDocs; CDocument0 m_wdDoc; CSelection m_wdSel; CRange m_wdRange; CnlineShapes m_wdInlineShapes; CnlineShape m_wdInlineShape; public: CCreateWordReport(); virtual ~CCreateWordReport(); public: //操作 //**********************创建新文档******************************************* BOOL CreateApp(); //创建一个新的WORD应用程序 BOOL CreateDocuments(); //创建一个新的Word文档集合 BOOL CreateDocument(); //创建一个新的Word文档 BOOL Create(); //创建新的WORD应用程序并创建一个新的文档 void ShowApp(); //显示WORD文档 void HideApp(); //隐藏word文档 //**********************打开文档********************************************* BOOL OpenDocument(CString fileName);//打开已经存在的文档。 BOOL Open(CString fileName); //创建新的WORD应用程序并打开一个已经存在的文档。 BOOL SetActiveDocument(short i); //设置当前激活的文档。 //**********************保存文档********************************************* BOOL SaveDocument(); //文档是以打开形式,保存。 BOOL SaveDocumentAs(CString fileName);//文档以创建形式,保存。 BOOL CloseDocument(); void CloseApp(); //**********************文本书写操作***************************************** void WriteText(CString szText); //当前光标处写文本 void WriteNewLineText(CString szText, int nLineCount = 1); //换N行写字 void WriteEndLine(CString szText); //文档结尾处写文本 void WholeStory(); //全选文档内容 void Copy(); //复制文本内容到剪贴板 void InsertFile(CString fileName); //将本地的文件全部内容写入到当前文档的光标处。 void InsertTable(int nRow, int nColumn, CTable0& wdTable); //**********************图片插入操作***************************************** void InsertShapes(CString fileName);//在当前光标的位置插入图片 //**********************超链接插入操作***************************************** void InsertHyperlink(CString fileLink);//超级链接地址,可以是相对路径。 //***********************表格操作表格操作********************************** BOOL InsertTableToMarkBook(const CString csMarkName, int nRow, int nColumn, CTable0& wdTable); //表格行数与列数 BOOL WriteDataToTable(CTable0& wdTable, int nRow, int nColumn, const CString &csData); //往表格中写入输入 };BOOL CCreateWordReport::CreateApp() { if (FALSE == m_wdApp.CreateDispatch("word.application")) { AfxMessageBox("Application创建失败,请确保安装了word 2000或以上版本!", MB_OK|MB_ICONWARNING); return FALSE; } return TRUE; } BOOL CCreateWordReport::CreateDocuments() { if (FALSE == CreateApp()) { return FALSE; } m_wdDocs = m_wdApp.get_Documents(); if (!m_wdDocs.m_lpDispatch) { AfxMessageBox("Documents创建失败!", MB_OK|MB_ICONWARNING); return FALSE; } return TRUE; } BOOL CCreateWordReport::CreateDocument() { if (!m_wdDocs.m_lpDispatch) { AfxMessageBox("Documents为空!", MB_OK|MB_ICONWARNING); return FALSE; } COleVariant varTrue(short(1),VT_BOOL),vOptional((long)DISP_E_PARAMNOTFOUND, VT_ERROR); CComVariant Template(_T("")); //没有使用WORD的文档模板 CComVariant NewTemplate(false),DocumentType(0),Visible; m_wdDocs.Add(&Template,&NewTemplate,&DocumentType,&Visible); //得到document变量 m_wdDoc = m_wdApp.get_ActiveDocument(); if (!m_wdDoc.m_lpDispatch) { AfxMessageBox("Document获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } //得到selection变量 m_wdSel = m_wdApp.get_Selection(); if (!m_wdSel.m_lpDispatch) { AfxMessageBox("Select获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } //得到Range变量 m_wdRange = m_wdDoc.Range(vOptional,vOptional); if(!m_wdRange.m_lpDispatch) { AfxMessageBox("Range获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } return TRUE; } BOOL CCreateWordReport::Create() { if (FALSE == CreateDocuments()) { return FALSE; } return CreateDocument(); } BOOL CCreateWordReport::OpenDocument(CString fileName) { if (!m_wdDocs.m_lpDispatch) { AfxMessageBox("Documents为空!", MB_OK|MB_ICONWARNING); return FALSE; } COleVariant vTrue((short)TRUE), vFalse((short)FALSE), vOptional((long)DISP_E_PARAMNOTFOUND, VT_ERROR), vZ((short)0); COleVariant vFileName(_T(fileName)); //得到document变量 m_wdDoc = m_wdDocs.Open( vFileName, // FileName vTrue, // Confirm Conversion. vFalse, // ReadOnly. vFalse, // AddToRecentFiles. vOptional, // PasswordDocument. vOptional, // PasswordTemplate. vOptional, // Revert. vOptional, // WritePasswordDocument. vOptional, // WritePasswordTemplate. vOptional, // Format. // Last argument for Word 97 vOptional, // Encoding // New for Word 2000/2002 vOptional, // Visible /*如下4个是word2003需要的参数。本版本是word2000。*/ vOptional, // OpenAndRepair vZ, // DocumentDirection wdDocumentDirection LeftToRight vOptional, // NoEncodingDialog vOptional ); if (!m_wdDoc.m_lpDispatch) { AfxMessageBox("Document获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } //得到selection变量 m_wdSel = m_wdApp.get_Selection(); if (!m_wdSel.m_lpDispatch) { AfxMessageBox("Select获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } //得到全部DOC的Range变量 m_wdRange = m_wdDoc.Range(vOptional,vOptional); if(!m_wdRange.m_lpDispatch) { AfxMessageBox("Range获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } return TRUE; } BOOL CCreateWordReport::Open(CString fileName) { if (FALSE == CreateDocuments()) { return FALSE; } return OpenDocument(fileName); } BOOL CCreateWordReport::SetActiveDocument(short i) { COleVariant vIndex(_T(i)),vOptional((long)DISP_E_PARAMNOTFOUND, VT_ERROR); m_wdDoc.AttachDispatch(m_wdDocs.Item(vIndex)); m_wdDoc.Activate(); if (!m_wdDoc.m_lpDispatch) { AfxMessageBox("Document获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } //得到selection变量 m_wdSel = m_wdApp.get_Selection(); if (!m_wdSel.m_lpDispatch) { AfxMessageBox("Select获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } //得到全部DOC的Range变量 m_wdRange = m_wdDoc.Range(vOptional,vOptional); if(!m_wdRange.m_lpDispatch) { AfxMessageBox("Range获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } // HideApp(); return TRUE; } BOOL CCreateWordReport::SaveDocument() { if (!m_wdDoc.m_lpDispatch) { AfxMessageBox("Document获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } m_wdDoc.Save(); return TRUE; } BOOL CCreateWordReport::SaveDocumentAs(CString fileName) { if (!m_wdDoc.m_lpDispatch) { AfxMessageBox("Document获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } COleVariant covOptional((long)DISP_E_PARAMNOTFOUND,VT_ERROR); COleVariant varZero((short)0); COleVariant varTrue(short(1),VT_BOOL); COleVariant varFalse(short(0),VT_BOOL); COleVariant vFileName(_T(fileName)); m_wdDoc.SaveAs( vFileName, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional, covOptional ); return TRUE; } BOOL CCreateWordReport::CloseDocument() { COleVariant vTrue((short)TRUE), vFalse((short)FALSE), vOptional((long)DISP_E_PARAMNOTFOUND, VT_ERROR); m_wdDoc.Close(vFalse, // SaveChanges. vTrue, // OriginalFormat. vFalse // RouteDocument. ); m_wdDoc.AttachDispatch(m_wdApp.get_ActiveDocument()); if (!m_wdDoc.m_lpDispatch) { AfxMessageBox("Document获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } //得到selection变量 m_wdSel = m_wdApp.get_Selection(); if (!m_wdSel.m_lpDispatch) { AfxMessageBox("Select获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } //得到全部DOC的Range变量 m_wdRange = m_wdDoc.Range(vOptional,vOptional); if(!m_wdRange.m_lpDispatch) { AfxMessageBox("Range获取失败!", MB_OK|MB_ICONWARNING); return FALSE; } return TRUE; } void CCreateWordReport::CloseApp() { COleVariant vTrue((short)TRUE), vFalse((short)FALSE), vOptional((long)DISP_E_PARAMNOTFOUND, VT_ERROR); m_wdDoc.Save(); m_wdApp.Quit(vFalse, // SaveChanges. vTrue, // OriginalFormat. vFalse // RouteDocument. ); //释放内存申请资源 m_wdInlineShape.ReleaseDispatch(); m_wdInlineShapes.ReleaseDispatch(); //m_wdTb.ReleaseDispatch(); m_wdRange.ReleaseDispatch(); m_wdSel.ReleaseDispatch(); //m_wdFt.ReleaseDispatch(); m_wdDoc.ReleaseDispatch(); m_wdDocs.ReleaseDispatch(); m_wdApp.ReleaseDispatch(); } void CCreateWordReport::WriteText(CString szText) { m_wdSel.TypeText(szText); } void CCreateWordReport::WriteNewLineText(CString szText, int nLineCount /* = 1 */) { int i; if (nLineCount <= 0) { nLineCount = 0; } for (i = 0; i < nLineCount; i++) { m_wdSel.TypeParagraph(); } WriteText(szText); } void CCreateWordReport::WriteEndLine(CString szText) { m_wdRange.InsertAfter(szText); } void CCreateWordReport::WholeStory() { m_wdRange.WholeStory(); } void CCreateWordReport::Copy() { m_wdRange.CopyAsPicture(); } void CCreateWordReport::InsertFile(CString fileName) { COleVariant vFileName(fileName), vTrue((short)TRUE), vFalse((short)FALSE), vOptional((long)DISP_E_PARAMNOTFOUND, VT_ERROR), vNull(_T("")); /* void InsertFile(LPCTSTR FileName, VARIANT* Range, VARIANT* ConfirmConversions, VARIANT* Link, VARIANT* Attachment); */ m_wdSel.InsertFile( fileName, vNull, vFalse, vFalse, vFalse ); } void CCreateWordReport::InsertShapes(CString fileName) { COleVariant vTrue((short)TRUE), vFalse((short)FALSE), vOptional((long)DISP_E_PARAMNOTFOUND, VT_ERROR); m_wdInlineShapes=m_wdSel.get_InlineShapes(); m_wdInlineShape=m_wdInlineShapes.AddPicture(fileName,vFalse,vTrue,vOptional); } void CCreateWordReport::InsertHyperlink(CString fileLink) { COleVariant vAddress(_T(fileLink)),vSubAddress(_T("")); CRange aRange = m_wdSel.get_Range(); CHyperlinks vHyperlinks(aRange.get_Hyperlinks()); vHyperlinks.Add( aRange, //Object,必需。转换为超链接的文本或图形。 vAddress, //Variant 类型,可选。指定的链接的地址。此地址可以是电子邮件地址、Internet 地址或文件名。请注意,Microsoft Word 不检查该地址的正确性。 vSubAddress, //Variant 类型,可选。目标文件内的位置名,如书签、已命名的区域或幻灯片编号。 vAddress, //Variant 类型,可选。当鼠标指针放在指定的超链接上时显示的可用作“屏幕提示”的文本。默认值为 Address。 vAddress, //Variant 类型,可选。指定的超链接的显示文本。此参数的值将取代由 Anchor 指定的文本或图形。 vSubAddress //Variant 类型,可选。要在其中打开指定的超链接的框架或窗口的名字。 ); aRange.ReleaseDispatch(); vHyperlinks.ReleaseDispatch(); }这样我们就封装好了一些基本的操作,其实这些操作都是我自己根据网上的资料以及VB宏转化而来得到的代码。特殊操作在这里主要介绍一些比较骚的操作,这也是这篇文章主要有用的内容,前面基本操作网上都有源代码直接拿来用就OK了,这里的骚操作是我在项目中使用的主要操作,应该有应用价值。先请各位仔细想想,如果我们要根据前面的代码,从0开始完全用代码生成一个完整的报表是不是很累,而且一般报表都会包含一些通用的废话,这些话基本不会变化。如果将这些写到代码里面,如果后面这些话变了,我们就要修改并重新编译,是不是很麻烦。所以这里介绍的第一个操作就是利用模板和书签在合适的位置插入内容。书签的使用首先我们在Word中的适当位置创建一个标签,至于如何创建标签,请自行百度。然后在代码中的思路就是在文档中查找我们的标签,再获取光标的位置,最后就是在该位置处添加相应的内容了,这里我们举一个在光标位置插入文本的例子:void CCreateWordReport::WriteTextToBookMark(const CString& csMarkName, const CString& szText) { CBookmarks bks = m_wdDoc.get_Bookmarks(); //获取文档中的所有书签 CBookmark0 bk; COleVariant bk_name(csMarkName); bk = bks.Item(&bk_name); //查询对应名称的书签 CRange hRange = bk.get_Range(); //获取书签位置 if (hRange != NULL) { hRange.put_Text(szText); //在该位置处插入文本 } //最后不要忘记清理相关资源 hRange.ReleaseDispatch(); bk.ReleaseDispatch(); bks.ReleaseDispatch(); }表格的使用在word报表中表格应该是一个重头戏,表格中常用的接口如下:CTables0: 表格集合CTable0: 某个具体的表格,一般通过CTables来创建CTableCColumn: 表格列对象CRow:表格行对象CCel:表格单元格对象创建表格一般的操作如下:void CCreateWordReport::InsertTable(int nRow, int nColumn, CTable0& wdTable) { VARIANT vtDefault; COleVariant vtAuto; vtDefault.vt = VT_INT; vtDefault.intVal = 1; vtAuto.vt = VT_INT; vtAuto.intVal = 0; CTables0 wordtables = m_wdDoc.get_Tables(); wdTable = wordtables.Add(m_wdSel.get_Range(), nRow, nColumn, &vtDefault, &vtAuto); wordtables.ReleaseDispatch(); }往表格中写入内容的操作如下:BOOL CCreateWordReport::WriteDataToTable(CTable0& wdTable, int nRow, int nColumn, const CString &csData) { CCell cell = wdTable.Cell(nRow, nColumn); cell.Select(); //将光标移动到单元格 m_wdSel.TypeText(csData); cell.ReleaseDispatch(); return TRUE; }合并单元格的操作如下:CTable0 wdTable; InsertTable(5, 3, wdTable); //创建一个5行3列的表格 CCell cell = wdTable.Cell(1, 1); //获得第一行第一列的单元格 //设置第二列列宽 CColumns0 columns = wdTable.get_Columns(); CColumn col; col.AttachDispatch(columns.Item(2)); col.SetWidth(40, 1); cell.Merge(wdTable.Cell(5, 1)); //合并单元格,一直合并到第5行的第1列。 cell.SetWidth(30, 1); cell.ReleaseDispatch();合并单元格用的是Merge函数,该函数的参数是一个单元格对象,表示合并结束的单元格。这里合并类似于我们画矩形时提供的左上角坐标和右下角坐标移动光标跳出表格当时由于需要连续的生成多个表格,当时我将前一个表格的数据填完,光标位于最后一个单元格里面,这个时候如果再插入的时候会在这个单元格里面插入表格,这个时候需要我手动向下移动光标,让光标移除到表格外。移动光标的代码如下:m_wdSel.MoveDown(&COleVariant((short)wdLine), &COleVariant((short)1), &COleVariant((short)wdNULL)); 这里wdLine 是word相关接口定义的,表示希望以何种单位来移动,这里我是以行为单位。后面的1表示移动1行。但是我发现在面临换页的时候一次移动根本移动不出来,这个时候我又添加了一行这样的代码移动两行。但是问题又出现了,这一系列表格后面跟着另一个大标题,多移动几次之后可能会造成它移动到大标题的位置,而破坏我原来定义的模板,这个时候该怎么办呢?我采取的办法是,判断当前光标是否在表格中,如果是则移动一行,知道出了表格。这里的代码如下://移动光标,直到跳出表格外 while (TRUE) { m_wdSel.MoveDown(&COleVariant((short)wdLine), &COleVariant((short)1), &COleVariant((short)wdNULL)); m_wdSel.Collapse(&COleVariant((short)wdCollapseStart)); if (!m_wdSel.get_Information((long)wdWithInTable).boolVal) { break; } }样式的使用在使用样式的时候当然也可以用代码来定义,但是我们可以采取另一种方式,我们可以事先在模板文件中创建一系列样式,然后在需要的时候直接定义段落或者文本的样式即可m_wdSel.put_Style(COleVariant("二级标题")); //在当前光标处的样式定义为二级标题样式,这里的二级标题样式是我们在word中事先定义好的 m_wdSel.TypeText(csTitle); //在当前位置输出文本 m_wdSel.TypeParagraph(); //插入段落,这里主要为了换行,这个时候光标也会跟着动 m_wdSel.put_Style(COleVariant("正文")); //定义此处样式为正文样式 m_wdSel.TypeText(csText;插入图表我自己尝试用word生成的图表样式还可以,但是用代码插入的时候,样式就特别丑,这里没有办法,我采用GDI+绘制了一个饼图,然后将图片插入word中。BOOL CCreateWordReport::DrawVulInforPic(const CString& csMarkName, int nVulCnt, int nVulCris, int nHigh, int nMid, int nLow, int nPossible) { CBookmarks bks = m_wdDoc.get_Bookmarks(); COleVariant bk_name(csMarkName); CBookmark0 bk = bks.Item(&bk_name); bk.Select(); CnlineShapes isps = m_wdSel.get_InlineShapes(); COleVariant vFalse((short)FALSE); COleVariant vNull(""); COleVariant vOptional((long)DISP_E_PARAMNOTFOUND,VT_ERROR); //创建一个与桌面环境兼容的内存DC HWND hWnd = GetDesktopWindow(); HDC hDc = GetDC(hWnd); HDC hMemDc = CreateCompatibleDC(hDc); HBITMAP hMemBmp = CreateCompatibleBitmap(hDc, PICTURE_WIDTH + GLOBAL_MARGIN, PICTURE_LENGTH + 2 * GLOBAL_MARGIN + LENGED_BORDER_LENGTH); SelectObject(hMemDc, hMemBmp); //绘制并保存图表 DrawPie(hMemDc, nVulCnt, nVulCris, nHigh, nMid, nLow, nPossible); COleVariant vTrue((short)TRUE); CnlineShape isp=isps.AddPicture("D:\\Program\\WordReport\\WordReport\\test.png",vFalse,vTrue,vOptional); //以图片的方式插入图表 //设置图片的大小 isp.put_Height(141); isp.put_Width(423); bks.ReleaseDispatch(); bk.ReleaseDispatch(); isps.ReleaseDispatch(); isp.ReleaseDispatch(); DeleteObject(hMemDc); DeleteDC(hMemDc); ReleaseDC(hWnd, hDc); return TRUE; }最后,各个接口的参数可以参考下面的链接:.net Word office组件接口文档 -
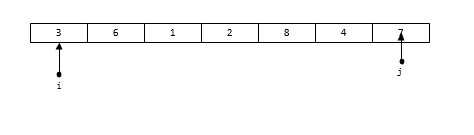
 算法与数据结构(七):快速排序 在上一篇中,回顾了一下针对选择排序的优化算法——堆排序。堆排序的时间复杂度为O(nlogn),而快速排序的时间复杂度也是O(nlogn)。但是快速排序在同为O(n*logn)的排序算法中,效率也是相对较高的,而且快速排序使用了算法中一个十分经典的思想——分治法;因此掌握快速排序还是很有必要的。快速排序的基本思想如下:在一组无序元素中,找到一个数作为基准数。将大于它的数全部移动到它的右侧,小于它的全部移动到右侧。在分成的两个区中,再次重复1到2 的步骤,直到所有的数全部有序下面还是来看一个例子[3,6,1,2,8,4,7]首先选取一个基准数,一般选择序列最左侧的数为基准数,也就是3,将小于3的数移动到3的左边,大于3的移动到3的右边,得到如下的序列[2,1,3,6,8,4,7]接着针对左侧的[2, 1] 这个序列和 [6, 8, ,4, 7]这两个序列再次执行这种操作,直到所有的数都变为有序为止。知道了具体的思路下面就是写算法了。void QSort(int a[], int n) { int nIdx = adjust(a, 0, n -1); //针对调整之后的数据左右两侧序列都再次进行调整 if(nIdx != -1) { QSort(&a[0], nIdx); QSort(&a[nIdx + 1], n - nIdx - 1); } }这里定义了一个函数作为快速排序的函数,函数需要传入序列的首地址以及序列中间元素的长度。在排序函数中只需要关注如何进行调整即可。这里进行了一个判断,当调整函数返回-1时表示不需要调整,也就是说此时已经都是有序的了,这个时候就不需要调整了。程序的基本框架已经完成了,剩下的就是如何编写调整函数了。调整的算法如下:首先定义两个指针,指向最右侧和最左侧,最左侧指针指向基准数所在位置先从右往左扫描,当发现右侧数小于基准值时,将基准值位置的数替换为该数,并且立刻从左往右扫描,直到找到一个数大于基准值,再次进行替换接着再次从右往左扫描,直到找到小于基准数的值;并再次改变扫描顺序,直到调整完毕最后直到两个指针重合,此时重合的位置就是基准值所在位置根据这个思路,可以编写如下代码int QuickSort(int a[], int nLow, int nHigh) { if (nLow >= nHigh) { return -1; } int tmp = a[nLow]; int i = nLow; int j = nHigh; while (i != j) { //先从右往左扫描,只到找到比基准值小的数 //将该数放到基准值的左侧 while (a[j] > tmp && j > i) { j--; } if (a[j] < tmp) { a[i]= a[j]; i++; } //接着从左往右扫描,直到找到比基准值大的数 //将该数放入到基准值的右侧 while (a[i] < tmp && i < j) { i++; } if (a[i] > tmp) { a[j] = a[i]; j--; } } a[i] = tmp; return i; }到此已经完成了快速排序的算法编写了。在有大量的数据需要进行排序时快速排序的效果比较好,如果数据量小,或者排序的序列已经是一个逆序的有序序列,它退化成O(n^2)。快速排序是一个不稳定的排序算法。
算法与数据结构(七):快速排序 在上一篇中,回顾了一下针对选择排序的优化算法——堆排序。堆排序的时间复杂度为O(nlogn),而快速排序的时间复杂度也是O(nlogn)。但是快速排序在同为O(n*logn)的排序算法中,效率也是相对较高的,而且快速排序使用了算法中一个十分经典的思想——分治法;因此掌握快速排序还是很有必要的。快速排序的基本思想如下:在一组无序元素中,找到一个数作为基准数。将大于它的数全部移动到它的右侧,小于它的全部移动到右侧。在分成的两个区中,再次重复1到2 的步骤,直到所有的数全部有序下面还是来看一个例子[3,6,1,2,8,4,7]首先选取一个基准数,一般选择序列最左侧的数为基准数,也就是3,将小于3的数移动到3的左边,大于3的移动到3的右边,得到如下的序列[2,1,3,6,8,4,7]接着针对左侧的[2, 1] 这个序列和 [6, 8, ,4, 7]这两个序列再次执行这种操作,直到所有的数都变为有序为止。知道了具体的思路下面就是写算法了。void QSort(int a[], int n) { int nIdx = adjust(a, 0, n -1); //针对调整之后的数据左右两侧序列都再次进行调整 if(nIdx != -1) { QSort(&a[0], nIdx); QSort(&a[nIdx + 1], n - nIdx - 1); } }这里定义了一个函数作为快速排序的函数,函数需要传入序列的首地址以及序列中间元素的长度。在排序函数中只需要关注如何进行调整即可。这里进行了一个判断,当调整函数返回-1时表示不需要调整,也就是说此时已经都是有序的了,这个时候就不需要调整了。程序的基本框架已经完成了,剩下的就是如何编写调整函数了。调整的算法如下:首先定义两个指针,指向最右侧和最左侧,最左侧指针指向基准数所在位置先从右往左扫描,当发现右侧数小于基准值时,将基准值位置的数替换为该数,并且立刻从左往右扫描,直到找到一个数大于基准值,再次进行替换接着再次从右往左扫描,直到找到小于基准数的值;并再次改变扫描顺序,直到调整完毕最后直到两个指针重合,此时重合的位置就是基准值所在位置根据这个思路,可以编写如下代码int QuickSort(int a[], int nLow, int nHigh) { if (nLow >= nHigh) { return -1; } int tmp = a[nLow]; int i = nLow; int j = nHigh; while (i != j) { //先从右往左扫描,只到找到比基准值小的数 //将该数放到基准值的左侧 while (a[j] > tmp && j > i) { j--; } if (a[j] < tmp) { a[i]= a[j]; i++; } //接着从左往右扫描,直到找到比基准值大的数 //将该数放入到基准值的右侧 while (a[i] < tmp && i < j) { i++; } if (a[i] > tmp) { a[j] = a[i]; j--; } } a[i] = tmp; return i; }到此已经完成了快速排序的算法编写了。在有大量的数据需要进行排序时快速排序的效果比较好,如果数据量小,或者排序的序列已经是一个逆序的有序序列,它退化成O(n^2)。快速排序是一个不稳定的排序算法。 -
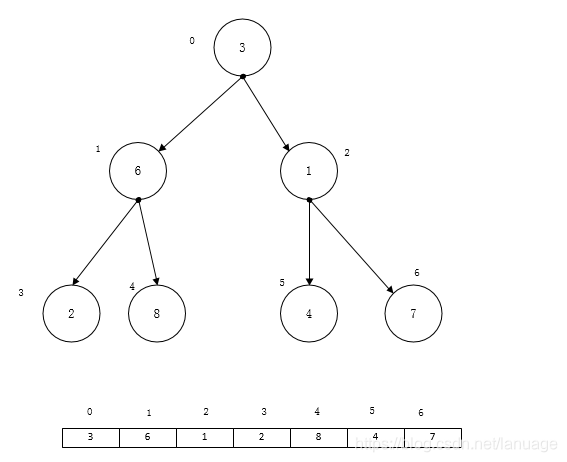
 算法与数据结构(六):堆排序 上一次说到了3种基本的排序算法,三种基本的排序算法时间复杂度都是O(n^2),虽然比较简单,但是效率相对较差,因此后续有许多相应的改进算法,这次主要说说堆排序算法。堆排序算法是对选择排序的一种优化。那么什么是堆呢?堆是一种树形结构。在维基百科上的定义是这样的“给定堆中任意节点 P 和 C,若 P 是 C 的母节点,那么 P 的值会小于等于(或大于等于) C 的值”。这句话通俗一点就是,树的根节点需要大于(小于)它的孩子节点,而每个左右子树都满足这个条件。当树的根节点大于它的左右孩子节点时称为大顶推,否则称为小顶堆。排序算法的思路是这样的,首先将序列中的元素组织成一个大顶堆,将树的根节点放到序列的最后面,然后将剩余的元素再组织成一个大顶堆,然后放到倒数第二个位置,以此类推。先假定它们的对应关系如下图所示:我们从树的最后一个非叶子节点开始,从这个子树中选择最大的一个数,将它交换到子树的根节点,也就是如下图所示接着再从后往前查找下一个非叶子节点经过这样一轮,一直调整到树的根节点,让后将根节点放到序列的最后一个元素,接着再将剩余元素重新组织为一个新的堆,直到所有元素都完成排序现在已经对堆排序的基本思路有了一定的了解,在写代码之前需要建立树节点与它在序列中的相关位置做一个对应关系,假设一个非叶子节点在序列中的位置为n,那么它的两个子节点分别是2n + 1与 2n + 2。而且小于n的一定是位于n前方的非叶子节点,所以在调整堆时,从n开始一直到0,前面的一定是非叶子节点,根据这点可以写出这样的代码void HeapSort(int a[], int nLength) { //从最后一个非叶子节点开始调整 for (int n = nLength / 2 - 1; n >= 0; n--) { HeapAdjust(a, n, nLength); } for (int n = nLength - 1; n > 0; n--) { //取堆顶与最后一个叶子节点互换 int tmp = a[0]; a[0] = a[n]; a[n] = tmp; //调整剩余堆 HeapAdjust(a, 0, n); } }上述代码首先取最后一个叶子节点,对所有非叶子节点进行调整,得到堆顶的最大元素。然后将最大元素与序列最后一个做交换,接着使用循环,对序列中剩余元素进行同样的操作。调整堆时,首先比较子树的根节点与它下面的所有子节点,并保存最大数的位置,然后将最大数与根节点的数进行交换,这样一直进行,直到完成了堆根节点的交换。void HeapAdjust(int a[], int nIdx, int nLength) { int child = 0; //child 保存当前最大数的下标 while (2 * nIdx + 1 < nLength) { child = 2 * nIdx + 1; //先找子节点的最大值(保证存在右节点的情况下) if (child < nLength - 1 && a[child] < a[child + 1]) { child++; } if (a[nIdx] < a[child]) { int tmp = a[nIdx]; a[nIdx] = a[child]; a[child] = tmp; }else { break; } //如果进行了交换,为了防止对子节点对应子树的破坏,要对子树也进行调整 nIdx = child; } }从算法上来看,它循环的次数与堆的深度有关,而二叉树的深度应该是log2(n) 向下取整,所以调整的时候需要进行log2(n)次调整,而外层需要从0一直到n - 1的位置每次都需要重组堆并进行调整,所以它的时间复杂度应该为O(nlogn), 它在效率上比选择排序要高,它的速度主要体现在每次查找选择最大的数这个方面。
算法与数据结构(六):堆排序 上一次说到了3种基本的排序算法,三种基本的排序算法时间复杂度都是O(n^2),虽然比较简单,但是效率相对较差,因此后续有许多相应的改进算法,这次主要说说堆排序算法。堆排序算法是对选择排序的一种优化。那么什么是堆呢?堆是一种树形结构。在维基百科上的定义是这样的“给定堆中任意节点 P 和 C,若 P 是 C 的母节点,那么 P 的值会小于等于(或大于等于) C 的值”。这句话通俗一点就是,树的根节点需要大于(小于)它的孩子节点,而每个左右子树都满足这个条件。当树的根节点大于它的左右孩子节点时称为大顶推,否则称为小顶堆。排序算法的思路是这样的,首先将序列中的元素组织成一个大顶堆,将树的根节点放到序列的最后面,然后将剩余的元素再组织成一个大顶堆,然后放到倒数第二个位置,以此类推。先假定它们的对应关系如下图所示:我们从树的最后一个非叶子节点开始,从这个子树中选择最大的一个数,将它交换到子树的根节点,也就是如下图所示接着再从后往前查找下一个非叶子节点经过这样一轮,一直调整到树的根节点,让后将根节点放到序列的最后一个元素,接着再将剩余元素重新组织为一个新的堆,直到所有元素都完成排序现在已经对堆排序的基本思路有了一定的了解,在写代码之前需要建立树节点与它在序列中的相关位置做一个对应关系,假设一个非叶子节点在序列中的位置为n,那么它的两个子节点分别是2n + 1与 2n + 2。而且小于n的一定是位于n前方的非叶子节点,所以在调整堆时,从n开始一直到0,前面的一定是非叶子节点,根据这点可以写出这样的代码void HeapSort(int a[], int nLength) { //从最后一个非叶子节点开始调整 for (int n = nLength / 2 - 1; n >= 0; n--) { HeapAdjust(a, n, nLength); } for (int n = nLength - 1; n > 0; n--) { //取堆顶与最后一个叶子节点互换 int tmp = a[0]; a[0] = a[n]; a[n] = tmp; //调整剩余堆 HeapAdjust(a, 0, n); } }上述代码首先取最后一个叶子节点,对所有非叶子节点进行调整,得到堆顶的最大元素。然后将最大元素与序列最后一个做交换,接着使用循环,对序列中剩余元素进行同样的操作。调整堆时,首先比较子树的根节点与它下面的所有子节点,并保存最大数的位置,然后将最大数与根节点的数进行交换,这样一直进行,直到完成了堆根节点的交换。void HeapAdjust(int a[], int nIdx, int nLength) { int child = 0; //child 保存当前最大数的下标 while (2 * nIdx + 1 < nLength) { child = 2 * nIdx + 1; //先找子节点的最大值(保证存在右节点的情况下) if (child < nLength - 1 && a[child] < a[child + 1]) { child++; } if (a[nIdx] < a[child]) { int tmp = a[nIdx]; a[nIdx] = a[child]; a[child] = tmp; }else { break; } //如果进行了交换,为了防止对子节点对应子树的破坏,要对子树也进行调整 nIdx = child; } }从算法上来看,它循环的次数与堆的深度有关,而二叉树的深度应该是log2(n) 向下取整,所以调整的时候需要进行log2(n)次调整,而外层需要从0一直到n - 1的位置每次都需要重组堆并进行调整,所以它的时间复杂度应该为O(nlogn), 它在效率上比选择排序要高,它的速度主要体现在每次查找选择最大的数这个方面。 -
 算法与数据结构(五):基本排序算法 前面几篇基本上把基本的数据结构都回顾完了,现在开始回顾那些常见的排序算法。排序是将一组无序的数据根据某种规则重新排列成有序的这么一个过程,当时在大学需要我们手工自己实现的主要有三种:选择排序、插入排序和冒泡排序。因为它比较简单,所以这里把他们放到一起作为最基本的排序算法。插入排序插入排序的思路是这样的:首先假设{k1, k2, k3, ...., kn} 中第一个元素是一个有序序列,从k2 开始插入到前面有序序列的适当位置从而使之前的有序序列仍然保持有序这么说可能有点抽象,我们以一个实例来说明:假设现在有这么一组待排元素: 3,6,1,2,8,4,7;先假设第一个元素3 是一个有序序列,从后续序列中取出6这个元素插入到前面的有序序列,得到3, 6 这么一个有序序列,此时序列为:3, 6, 1, 2, 8, 4, 7现在3, 6 是一个有序序列,从之前的序列中取出1,插入到有序序列的合适位置,得到1, 3, 6 这么一个有序序列,此时序列为: 1, 3, 6, 2, 8, 4, 7接着从待排元素中取出2,插入到适当位置,得到有序序列 1, 2, 3, 6;此时序列为 1, 2, 3, 6, 8, 4, 7以此类推,直到所有元素都排列完成,下面是每次排序后生成的序列1) 3 6 1 2 8 4 72) 1 3 6 2 8 4 73) 1 2 3 6 8 4 74) 1 2 3 6 8 4 75) 1 2 3 4 6 8 76) 1 2 3 4 6 7 87) 1 2 3 4 6 7 8那么知道了这个算法的思想,下面就是考虑该如何将其转化为代码,由计算机帮助我们实现这些事了。首先这段代码至少有一层循环来依次取出序列中的待排元素,由于假定第一个元素已经是有序的,所以循环次数应该是n - 1次,而且从序列的第2个元素开始。for(int i = 1; i < n; i++) { //do something; }那么如何确定元素的适当位置呢,我们人从肉眼上来看肯定是可以看出来的,计算机并不知道啊。由于之前的序列肯定是有序的,所以这里我们只需要从前往后将有序序列中的数与待插入数比较,只要序列中的数大于待插入数,那么将带插入数插入到该数的前面就可以了。因为之前的序列是有序的,插入到该位置肯定能保证新插入数大于它之前的数但是小于它之后的数。这个时候我们可以写出这样一段伪代码for(int i = i; i < n; i++) { for(int j = 0; j < i; j++) { if(a[i] < a[j]) { //此时j就是插入的位置,插入即可 } } }同时在插入的时候需要考虑腾挪后续的元素,为了方便腾挪元素,应该从有序列表的后方向前面进行比较,在比较的同时进行元素的腾挪,直到找到位置,这个时候的代码应该替换为这样for(int i = i; i < n; i++) { int tmp = a[i]; int j = i - 1; //从有序列表的最后一个元素开始往前找 while(j >= 0 && tmp < a[j]) { a[j + 1] = a[j]; //将对应元素往后挪一个位置 j--; } a[j + 1] = tmp; }从算法上来看,插入排序是一种O(n^2)的算法选择排序选择排序是最好理解的一种算法,选择排序的基本思路是每次从待排序列中选择最大(或者最小)的一个,放到已排好的序列的最前面,形成一个新的有序序列,直到所有元素都完成排序仍然是之前的一个序列 3, 6, 1, 2, 8, 4, 7首先找到最小的数1,排到最前面:1, 6, 3, 2, 8, 4, 7再找到后续最小数2,排到1后面:1, 2, 3, 6, 8, 4, 7接着找到后续最小数3,排到2后面:1, 2, 3, 6, 8, 4, 7以此类推,得到每次排序后的序列:1) 1 6 3 2 8 4 72) 1 2 3 6 8 4 73) 1 2 3 6 8 4 74) 1 2 3 4 8 6 75) 1 2 3 4 6 8 76) 1 2 3 4 6 7 87) 1 2 3 4 6 7 8从上面来看,每次确定了最小数之后只需要将对应位置的数与这个最小数交换就完成了排序,这也是与插入排序不同的地方,插入排序在处理元素的时候采用腾挪的方式,而选择排序则直接采用交换,也就是说插入排序在处理未排序元素的时候并没有改变他们的位置,而选择排序则有可能修改他们的位置,因此我们说选择排序是一种不稳定的排序,而插入排序是稳定的排序.实现的算法如下:for (int i = 0; i < n - 1; i++) { int k = i; //k 表示当前剩余序列中最小数的位置 //该循环从当前剩余数中找到最小数位置 for (int j = i; j < n; j++) { if (a[j] < a[k]) { k = j; } } if (k != i) { int tmp = a[k]; a[k] = a[i]; a[i] = tmp; } }选择排序的时间复杂度仍然是 O(n^2)冒泡排序冒泡排序是在C语言课上讲到的一种排序方式,简单来说就是将待排序列中的数据从头开始两两比较,然后将大数交换到后面,这样每次循环之后总是大数沉到最后面,进行多次这样的循环,就能完成排序还是从 3, 6, 1, 2, 8, 4, 7 序列的排序开始首先3与6相比,6大,此时不用交换,接着,6与1比较,6大然后进行交换。接着6与2比较,再交换,6与8比较,不用交换,8与4比较需要交换,8与7比较需要交换,因此第一次冒泡的结果是3, 1, 2, 6, 4, 7, 8依次类推得到每次结果如下:1) 3 1 2 6 4 7 82) 1 2 3 4 6 7 83) 1 2 3 4 6 7 84) 1 2 3 4 6 7 85) 1 2 3 4 6 7 86) 1 2 3 4 6 7 87) 1 2 3 4 6 7 8实现的算法如下:for (int i = 0; i < nLength - 1; i++) { for (int j = 0; j < nLength - i - 1; j++) { if (a[j] > a[j + 1]) { int tmp = a[j]; a[j] = a[j+ 1]; a[j + 1] = tmp; } } }冒泡排序也是一个不稳定的排序算法,它的时间复杂度也是O(n^2)
算法与数据结构(五):基本排序算法 前面几篇基本上把基本的数据结构都回顾完了,现在开始回顾那些常见的排序算法。排序是将一组无序的数据根据某种规则重新排列成有序的这么一个过程,当时在大学需要我们手工自己实现的主要有三种:选择排序、插入排序和冒泡排序。因为它比较简单,所以这里把他们放到一起作为最基本的排序算法。插入排序插入排序的思路是这样的:首先假设{k1, k2, k3, ...., kn} 中第一个元素是一个有序序列,从k2 开始插入到前面有序序列的适当位置从而使之前的有序序列仍然保持有序这么说可能有点抽象,我们以一个实例来说明:假设现在有这么一组待排元素: 3,6,1,2,8,4,7;先假设第一个元素3 是一个有序序列,从后续序列中取出6这个元素插入到前面的有序序列,得到3, 6 这么一个有序序列,此时序列为:3, 6, 1, 2, 8, 4, 7现在3, 6 是一个有序序列,从之前的序列中取出1,插入到有序序列的合适位置,得到1, 3, 6 这么一个有序序列,此时序列为: 1, 3, 6, 2, 8, 4, 7接着从待排元素中取出2,插入到适当位置,得到有序序列 1, 2, 3, 6;此时序列为 1, 2, 3, 6, 8, 4, 7以此类推,直到所有元素都排列完成,下面是每次排序后生成的序列1) 3 6 1 2 8 4 72) 1 3 6 2 8 4 73) 1 2 3 6 8 4 74) 1 2 3 6 8 4 75) 1 2 3 4 6 8 76) 1 2 3 4 6 7 87) 1 2 3 4 6 7 8那么知道了这个算法的思想,下面就是考虑该如何将其转化为代码,由计算机帮助我们实现这些事了。首先这段代码至少有一层循环来依次取出序列中的待排元素,由于假定第一个元素已经是有序的,所以循环次数应该是n - 1次,而且从序列的第2个元素开始。for(int i = 1; i < n; i++) { //do something; }那么如何确定元素的适当位置呢,我们人从肉眼上来看肯定是可以看出来的,计算机并不知道啊。由于之前的序列肯定是有序的,所以这里我们只需要从前往后将有序序列中的数与待插入数比较,只要序列中的数大于待插入数,那么将带插入数插入到该数的前面就可以了。因为之前的序列是有序的,插入到该位置肯定能保证新插入数大于它之前的数但是小于它之后的数。这个时候我们可以写出这样一段伪代码for(int i = i; i < n; i++) { for(int j = 0; j < i; j++) { if(a[i] < a[j]) { //此时j就是插入的位置,插入即可 } } }同时在插入的时候需要考虑腾挪后续的元素,为了方便腾挪元素,应该从有序列表的后方向前面进行比较,在比较的同时进行元素的腾挪,直到找到位置,这个时候的代码应该替换为这样for(int i = i; i < n; i++) { int tmp = a[i]; int j = i - 1; //从有序列表的最后一个元素开始往前找 while(j >= 0 && tmp < a[j]) { a[j + 1] = a[j]; //将对应元素往后挪一个位置 j--; } a[j + 1] = tmp; }从算法上来看,插入排序是一种O(n^2)的算法选择排序选择排序是最好理解的一种算法,选择排序的基本思路是每次从待排序列中选择最大(或者最小)的一个,放到已排好的序列的最前面,形成一个新的有序序列,直到所有元素都完成排序仍然是之前的一个序列 3, 6, 1, 2, 8, 4, 7首先找到最小的数1,排到最前面:1, 6, 3, 2, 8, 4, 7再找到后续最小数2,排到1后面:1, 2, 3, 6, 8, 4, 7接着找到后续最小数3,排到2后面:1, 2, 3, 6, 8, 4, 7以此类推,得到每次排序后的序列:1) 1 6 3 2 8 4 72) 1 2 3 6 8 4 73) 1 2 3 6 8 4 74) 1 2 3 4 8 6 75) 1 2 3 4 6 8 76) 1 2 3 4 6 7 87) 1 2 3 4 6 7 8从上面来看,每次确定了最小数之后只需要将对应位置的数与这个最小数交换就完成了排序,这也是与插入排序不同的地方,插入排序在处理元素的时候采用腾挪的方式,而选择排序则直接采用交换,也就是说插入排序在处理未排序元素的时候并没有改变他们的位置,而选择排序则有可能修改他们的位置,因此我们说选择排序是一种不稳定的排序,而插入排序是稳定的排序.实现的算法如下:for (int i = 0; i < n - 1; i++) { int k = i; //k 表示当前剩余序列中最小数的位置 //该循环从当前剩余数中找到最小数位置 for (int j = i; j < n; j++) { if (a[j] < a[k]) { k = j; } } if (k != i) { int tmp = a[k]; a[k] = a[i]; a[i] = tmp; } }选择排序的时间复杂度仍然是 O(n^2)冒泡排序冒泡排序是在C语言课上讲到的一种排序方式,简单来说就是将待排序列中的数据从头开始两两比较,然后将大数交换到后面,这样每次循环之后总是大数沉到最后面,进行多次这样的循环,就能完成排序还是从 3, 6, 1, 2, 8, 4, 7 序列的排序开始首先3与6相比,6大,此时不用交换,接着,6与1比较,6大然后进行交换。接着6与2比较,再交换,6与8比较,不用交换,8与4比较需要交换,8与7比较需要交换,因此第一次冒泡的结果是3, 1, 2, 6, 4, 7, 8依次类推得到每次结果如下:1) 3 1 2 6 4 7 82) 1 2 3 4 6 7 83) 1 2 3 4 6 7 84) 1 2 3 4 6 7 85) 1 2 3 4 6 7 86) 1 2 3 4 6 7 87) 1 2 3 4 6 7 8实现的算法如下:for (int i = 0; i < nLength - 1; i++) { for (int j = 0; j < nLength - i - 1; j++) { if (a[j] > a[j + 1]) { int tmp = a[j]; a[j] = a[j+ 1]; a[j + 1] = tmp; } } }冒泡排序也是一个不稳定的排序算法,它的时间复杂度也是O(n^2) -
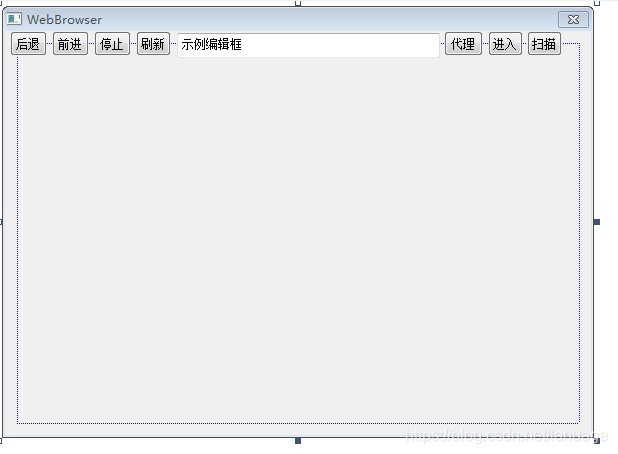
 使用miniblink 在程序中嵌入浏览器 最近公司产品中自定义浏览器比较老,打开一些支持h5 的站莫名报错,而且经常弹框。已经到了令人无法忍受的地步了,于是我想到了将内核由之前的IE 升级到Chromium。之前想到的是使用cef来做,而且网上的资源和教程也很多,后来在自己尝试的过程中发现使用cef时程序会莫名其妙的崩溃,特别是在关闭对话框的时候。我在网上找了一堆资料,尝试了各种版本未果,这个方案也就放弃了。后来又搜到了wke和miniblink,对比二者官方的文档和demo,我决定使用miniblink,毕竟我直接搜索wke browser 出来的都是miniblink,只有搜索wke github 才会有真正的wke,而且wke似乎没有api文档,最后miniblink是国人写的,文档都是中文而且又有专门的qq交流群,有问题可以咨询一下。什么是miniblinkminiblink 是由国内大神 龙泉寺扫地僧 针对chromium内核进行裁剪去掉了所有多余的部件,只保留最基本的排版引擎blink,而产生的一款号称全球小巧的浏览器内核项目,目前miniblink 保持了10M左右的极简大小,相比CEF 动辄几百M的大小确实小巧许多。而且能很好的支持H5等一些列新标准,同时它内嵌了Nodejs 支持electron。而且也支持各种语言调用。官方的地址如下为 https://weolar.github.io/miniblink/index.html使用miniblink说了这么多那么该怎么用呢?从官方的介绍来看,我们可以使用VS的向导程序生成一个普通的win32 窗口程序,然后生成的这些代码中将函数InitInstance 中的代码全部删除加上这么5句话wkeSetWkeDllPath(L"E:\\mycode\\miniblink49\\trunk\\out\\Release_vc6\\node.dll"); wkeInitialize(); wkeWebView window = wkeCreateWebWindow(WKE_WINDOW_TYPE_POPUP, NULL, 0, 0, 1080, 680); wkeLoadURL(window, "qq.com"); wkeShowWindow(window, TRUE);当然,使用这些函数需要下载它的SDK开发包,然后在对应位置包含wke.h。这些代码会生成一个窗口程序,具体的请敢兴趣的朋友自己去实践看看效果。或者编译运行一下它的demo程序。在对话框中使用现在我想在对话框中使用,那么该怎么办呢。首先也是先用MFC的向导生成一个对话框并编辑资源文件。最后我的对话框大概长成这样我会将按钮下面部分全部作为浏览器页面。我们在程序APP类的InitInstance函数 中初始化miniblink库,并在对话框被关闭后直接卸载miniblink的相关资源wkeSetWkeDllPath(L"node.dll"); wkeInitialize(); CWebBrowserDlg dlg = CWebBrowserDlg(); m_pMainWnd = dlg; INT_PTR nResponse = dlg.DoModal(); if (nResponse == IDOK) { // TODO: 在此放置处理何时用 // “确定”来关闭对话框的代码 } else if (nResponse == IDCANCEL) { // TODO: 在此放置处理何时用 // “取消”来关闭对话框的代码 } // 由于对话框已关闭,所以将返回 FALSE 以便退出应用程序, // 而不是启动应用程序的消息泵。 wkeFinalize();然后在主对话框类中新增一个成员变量用来保存miniblink的web视图的句柄wkeWebView m_web;我们在对话框的OnInitDialog函数中创建这么一个视图,用来加载百度的首页面GetClientRect(&rtClient); rtClient.top += 24; m_web = wkeCreateWebWindow(WKE_WINDOW_TYPE_CONTROL, *this, rtClient.left, rtClient.top, rtClient.right - rtClient.left, rtClient.bottom - rtClient.top); wkeLoadURL(m_web, "https://www.baidu.com"); wkeShowWindow(m_web, TRUE);至此我们已经能够生成一个简单的浏览器程序似乎到这已经差不多该结束了,但是现在我遇到了在整个程序完成期间最大的问题,那就是web页面无法响应键盘消息,我尝试过改成窗口程序,发现改了之后能正常运行,但是我要的是对话框啊。这么改只能证明这个库是没问题的。后来我在群里面发出了这样的疑问,有朋友告诉我说应该是wkeWebView没有接受到键盘消息,于是我打算处理主对话框的WM_KEYDOWN 和WM_KEYUP 以及WM_CHAR消息,根据官方的文档,应该是只需要拦截对话框的这三个消息,然后使用函数wkeFireKeyUpEvent、wkeFireKeyDownEvent、wkeFireKeyPressEvent函数分别向wkeWebView发送键盘消息就可以了.于是我在对应的处理函数中添加了相关代码//OnChar unsigned int flags = 0; if (nFlags & KF_REPEAT) flags |= WKE_REPEAT; if (nFlags & KF_EXTENDED) flags |= WKE_EXTENDED; wkeFireKeyPressEvent(m_web, nChar, flags, false);//OnKeyUp unsigned int flags = 0; if (nFlags & KF_REPEAT) flags |= WKE_REPEAT; if (nFlags & KF_EXTENDED) flags |= WKE_EXTENDED; wkeFireKeyUpEvent(m_web, virtualKeyCode, flags, false);//OnKeyDown unsigned int flags = 0; if (nFlags & KF_REPEAT) flags |= WKE_REPEAT; if (nFlags & KF_EXTENDED) flags |= WKE_EXTENDED; wkeFireKeyDownEvent(m_web, virtualKeyCode, flags, false);但是这么干,我通过调试发现它好像并没有进入到这些函数里面来,也就是说键盘消息不是由主对话框来处理的。那么现在只能在wkeWebView 对应的窗口中来处理了。那么怎么捕获这个窗口的消息呢,miniblink提供了函数wkeGetHostHWND 来根据视图的句柄获取对应窗口的句柄,那么现在的思路就是这样的:首先获取对应的窗口句柄然后通过SetWindowLong来修改窗口的窗口过程,然后在窗口过程中处理这些消息就行了。根据这个思路整理一下代码//在创建wkeWebView 之后来hook窗口过程 HWND hWnd = wkeGetHostHWND(m_web); g_OldProc = (WNDPROC)SetWindowLong(hWnd, GWL_WNDPROC, (LONG)MyWndProc); //为了能够在全局函数中使用对话框类的东西,我们为窗口绑定一个对话框类的指针 SetWindowLong(hWnd, GWL_USERDATA, this);接着在MyWndProc中处理对应的消息事件LRESULT CALLBACK MyWndProc(HWND hWnd, UINT uMsg, WPARAM wParam, LPARAM lParam) { CWebBrowserDlg* pDlg = (CWebBrowserDlg*)GetWindowLong(hWnd, GWL_USERDATA); if (NULL == pDlg) { return CallWindowProc(g_OldProc, hWnd, uMsg, wParam, lParam); } switch (uMsg) { case WM_KEYUP: { unsigned int virtualKeyCode = wParam; unsigned int flags = 0; if (HIWORD(lParam) & KF_REPEAT) flags |= WKE_REPEAT; if (HIWORD(lParam) & KF_EXTENDED) flags |= WKE_EXTENDED; wkeFireKeyDownEvent(pDlg->m_web, virtualKeyCode, flags, false); } break; case WM_KEYDOWN: { unsigned int virtualKeyCode = wParam; unsigned int flags = 0; if (HIWORD(lParam) & KF_REPEAT) flags |= WKE_REPEAT; if (HIWORD(lParam) & KF_EXTENDED) flags |= WKE_EXTENDED; wkeFireKeyUpEvent(pDlg->m_web, virtualKeyCode, flags, false); } break; case WM_CHAR: { unsigned int charCode = wParam; unsigned int flags = 0; if (HIWORD(lParam) & KF_REPEAT) flags |= WKE_REPEAT; if (HIWORD(lParam) & KF_EXTENDED) flags |= WKE_EXTENDED; wkeFireKeyPressEvent(pDlg->m_web, charCode, flags, false); } break; default: return CallWindowProc(g_OldProc, hWnd, uMsg, wParam, lParam); } return 0; }这样做之后我发现它虽然能够截取到这些消息并执行它,但是在调用wkeFireKeyPressEvent等函数之后仍然无法响应键盘消息。难道是wkeCreateWebWindow 创建出来的窗口不能做子窗口?带着这个疑问我根据官方文档尝试了一下使用wkeCreateWebView ,然后将它绑定到对应的窗口上,然后这个整体作为子窗口的方式。代码太长了,我就不放出来了,有兴趣的可以翻到本文尾部,我将这个demo项目放到的GitHub上。结果还是不行。这些函数仍然进不来。真的郁闷,难道要换方案?我这个时候已经开始准备换方案了,在编译wke 的时候心情极度烦躁,我在之前的程序上不停的敲击键盘,就听见“等~等~等~”。我靠!这不是想从模态对话框上切换回主页面时的那个声音吗?会不会是因为模态对话框的关系?这个时候我瞬间来了灵感。那就换吧,主要改一下APP类中相关代码,吧模态改成非模态的就行CWebBrowserDlg *dlg = new CWebBrowserDlg(); dlg->Create(IDD_WEBBROWSER_DIALOG); m_pMainWnd = dlg; INT_PTR nResponse = dlg->ShowWindow(SW_SHOW); if (nResponse == IDOK) { // TODO: 在此放置处理何时用 // “确定”来关闭对话框的代码 } else if (nResponse == IDCANCEL) { // TODO: 在此放置处理何时用 // “取消”来关闭对话框的代码 } // 由于对话框已关闭,所以将返回 FALSE 以便退出应用程序, // 而不是启动应用程序的消息泵。 //由于是非模态对话框,所以这里需要自己写消息环 MSG msg = { 0 }; while (GetMessage(&msg, NULL, 0, 0)) { TranslateMessage(&msg); DispatchMessageW(&msg); } delete dlg;卧槽,居然成功了,能正常相应了!为什么模态就不行呢,后来我在复盘的时候想到,应该是wkeWebView的窗口并没有做成那种严格意义上的子窗口,它是一个独立的,所以模态对话框把消息给拦截了不让传到其他的窗口导致的这个问题。这个也算是成功了。这个时候问题又来了,程序关不掉了,虽然说窗口是关了,但是程序并没有退出,后来调试发现,消息环没有退出。这个时候我想到应该是关闭时调用的是EndDialog。但是此时已经改成非模态了,需要最后调用DestroyWindow,那么这个地方就得去对话框的OnClose消息中改。void CWebBrowserDlg::OnClose() { // TODO: 在此添加消息处理程序代码和/或调用默认值 DestroyWindow(); //CDialog::OnClose(); }好了,这个时候基本已经完成了。就剩下一些按钮事件处理了。按钮事件的处理这里直接贴代码吧,基本只有几行,很容易看懂的void CWebBrowserDlg::OnBnClickedBtnBack() { // TODO: 在此添加控件通知处理程序代码 if (wkeCanGoBack(m_web)) { wkeGoBack(m_web); } } void CWebBrowserDlg::OnBnClickedBtnForward() { // TODO: 在此添加控件通知处理程序代码 if (wkeCanGoForward(m_web)) { wkeGoForward(m_web); } } void CWebBrowserDlg::OnBnClickedBtnStop() { // TODO: 在此添加控件通知处理程序代码 wkeStopLoading(m_web); } void CWebBrowserDlg::OnBnClickedBtnRefresh() { // TODO: 在此添加控件通知处理程序代码 wkeReload(m_web); } void CWebBrowserDlg::OnBnClickedBtnGo() { // TODO: 在此添加控件通知处理程序代码 CString csurl; GetDlgItem(IDC_EDIT_URL)->GetWindowText(csurl); wkeLoadURLW(m_web, csurl); } //设置代理 void CWebBrowserDlg::OnBnClickedBtnProxy() { CDlgProxySet dlgProxySet; dlgProxySet.DoModal(); wkeProxy proxy; proxy.type = WKE_PROXY_HTTP; USES_CONVERSION; strcpy_s(proxy.hostname, sizeof(proxy.hostname), T2A(dlgProxySet.csIP)); proxy.port = dlgProxySet.m_port; wkeSetProxy(&proxy); // TODO: 在此添加控件通知处理程序代码 }wkeView 的回调函数现在主体功能已经完成了,要跟浏览器类似,需要处理这样几个东西。第一个是url栏中的内容会根据当前主页面的url做调整,特别是针对302、301 跳转的情况。第二个是窗口的标题应该改为页面的标题;第三个是在某些页面中超链接用的是_blank,时应该能正常打开新窗口。为了实现这些目标,我们需要处理一些wkeView的事件,我们创建了wkeWebView 之后直接绑定这些事件wkeOnTitleChanged(m_web, wkeOnTitleChangedCallBack, this); //最后一个参数是传递用户数据,这里我们传递this指针进去 wkeOnURLChanged(m_web, wkeOnURLChangedCallBack, this); wkeOnNavigation(m_web, wkeOnNavigationCallBack, this); wkeOnCreateView(m_web, onBrowserCreateView, this);// 页面标题更改时调用此回调 void _cdecl wkeOnTitleChangedCallBack(wkeWebView webView, void* param, const wkeString title) { CWebBrowserDlg *pDlg = (CWebBrowserDlg*)param; if (NULL != pDlg) { pDlg->SetWindowText(wkeGetStringW(title)); } } //url变更时调用此回调 void _cdecl wkeOnURLChangedCallBack(wkeWebView webView, void* param, const wkeString url) { CWebBrowserDlg *pDlg = (CWebBrowserDlg*)param; if (NULL != pDlg) { pDlg->GetDlgItem(IDC_EDIT_URL)->SetWindowTextW(wkeGetStringW(url)); } } //网页开始浏览将触发回调, 这里主要是为了它能打开一些本地的程序 bool _cdecl wkeOnNavigationCallBack(wkeWebView webView, void* param, wkeNavigationType navigationType, const wkeString url) { const wchar_t* urlStr = wkeGetStringW(url); if (wcsstr(urlStr, L"exec://") == urlStr) { PROCESS_INFORMATION processInfo = { 0 }; STARTUPINFOW startupInfo = { 0 }; startupInfo.cb = sizeof(startupInfo); BOOL succeeded = CreateProcessW(NULL, (LPWSTR)urlStr + 7, NULL, NULL, FALSE, 0, NULL, NULL, &startupInfo, &processInfo); if (succeeded) { CloseHandle(processInfo.hProcess); CloseHandle(processInfo.hThread); } return false; } return true; } //网页点击a标签创建新窗口时将触发回调 wkeWebView _cdecl onBrowserCreateView(wkeWebView webView, void* param, wkeNavigationType navType, const wkeString urlStr, const wkeWindowFeatures* features) { const wchar_t* url = wkeGetStringW(urlStr); wkeWebView newWindow = wkeCreateWebWindow(WKE_WINDOW_TYPE_POPUP, NULL, features->x, features->y, features->width, features->height); wkeShowWindow(newWindow, true); return newWindow; }至此这个浏览器的demo就完成了。最后贴上对应的demo项目地址: https://github.com/aMonst/WebBrowserPS:最近有一位朋友发邮件告诉我说,wkeWebView 不能响应键盘消息与对话框是模态还是非模态无关,主要是要处理wkeWebView的WM_GETDLGCODE 消息,那位朋友给出的代码如下:switch(uMsg) { case WM_GETDLGCODE: return DLGC_WANTARROWS | DLGC_WANTALLKEYS | DLGC_WANTCHARS; }我试了一下,发现确实是这样,相比较我上面提出的改为非模态的方式来说,还是用模态对话框方便、毕竟MFC对话框程序本来就是非模态的。所以这里我将代码做了一下修改。并同步到了GitHub上。最后再次感谢那位发邮件告诉的朋友。。。。。参考资料miniblink API文档官方DEMO
使用miniblink 在程序中嵌入浏览器 最近公司产品中自定义浏览器比较老,打开一些支持h5 的站莫名报错,而且经常弹框。已经到了令人无法忍受的地步了,于是我想到了将内核由之前的IE 升级到Chromium。之前想到的是使用cef来做,而且网上的资源和教程也很多,后来在自己尝试的过程中发现使用cef时程序会莫名其妙的崩溃,特别是在关闭对话框的时候。我在网上找了一堆资料,尝试了各种版本未果,这个方案也就放弃了。后来又搜到了wke和miniblink,对比二者官方的文档和demo,我决定使用miniblink,毕竟我直接搜索wke browser 出来的都是miniblink,只有搜索wke github 才会有真正的wke,而且wke似乎没有api文档,最后miniblink是国人写的,文档都是中文而且又有专门的qq交流群,有问题可以咨询一下。什么是miniblinkminiblink 是由国内大神 龙泉寺扫地僧 针对chromium内核进行裁剪去掉了所有多余的部件,只保留最基本的排版引擎blink,而产生的一款号称全球小巧的浏览器内核项目,目前miniblink 保持了10M左右的极简大小,相比CEF 动辄几百M的大小确实小巧许多。而且能很好的支持H5等一些列新标准,同时它内嵌了Nodejs 支持electron。而且也支持各种语言调用。官方的地址如下为 https://weolar.github.io/miniblink/index.html使用miniblink说了这么多那么该怎么用呢?从官方的介绍来看,我们可以使用VS的向导程序生成一个普通的win32 窗口程序,然后生成的这些代码中将函数InitInstance 中的代码全部删除加上这么5句话wkeSetWkeDllPath(L"E:\\mycode\\miniblink49\\trunk\\out\\Release_vc6\\node.dll"); wkeInitialize(); wkeWebView window = wkeCreateWebWindow(WKE_WINDOW_TYPE_POPUP, NULL, 0, 0, 1080, 680); wkeLoadURL(window, "qq.com"); wkeShowWindow(window, TRUE);当然,使用这些函数需要下载它的SDK开发包,然后在对应位置包含wke.h。这些代码会生成一个窗口程序,具体的请敢兴趣的朋友自己去实践看看效果。或者编译运行一下它的demo程序。在对话框中使用现在我想在对话框中使用,那么该怎么办呢。首先也是先用MFC的向导生成一个对话框并编辑资源文件。最后我的对话框大概长成这样我会将按钮下面部分全部作为浏览器页面。我们在程序APP类的InitInstance函数 中初始化miniblink库,并在对话框被关闭后直接卸载miniblink的相关资源wkeSetWkeDllPath(L"node.dll"); wkeInitialize(); CWebBrowserDlg dlg = CWebBrowserDlg(); m_pMainWnd = dlg; INT_PTR nResponse = dlg.DoModal(); if (nResponse == IDOK) { // TODO: 在此放置处理何时用 // “确定”来关闭对话框的代码 } else if (nResponse == IDCANCEL) { // TODO: 在此放置处理何时用 // “取消”来关闭对话框的代码 } // 由于对话框已关闭,所以将返回 FALSE 以便退出应用程序, // 而不是启动应用程序的消息泵。 wkeFinalize();然后在主对话框类中新增一个成员变量用来保存miniblink的web视图的句柄wkeWebView m_web;我们在对话框的OnInitDialog函数中创建这么一个视图,用来加载百度的首页面GetClientRect(&rtClient); rtClient.top += 24; m_web = wkeCreateWebWindow(WKE_WINDOW_TYPE_CONTROL, *this, rtClient.left, rtClient.top, rtClient.right - rtClient.left, rtClient.bottom - rtClient.top); wkeLoadURL(m_web, "https://www.baidu.com"); wkeShowWindow(m_web, TRUE);至此我们已经能够生成一个简单的浏览器程序似乎到这已经差不多该结束了,但是现在我遇到了在整个程序完成期间最大的问题,那就是web页面无法响应键盘消息,我尝试过改成窗口程序,发现改了之后能正常运行,但是我要的是对话框啊。这么改只能证明这个库是没问题的。后来我在群里面发出了这样的疑问,有朋友告诉我说应该是wkeWebView没有接受到键盘消息,于是我打算处理主对话框的WM_KEYDOWN 和WM_KEYUP 以及WM_CHAR消息,根据官方的文档,应该是只需要拦截对话框的这三个消息,然后使用函数wkeFireKeyUpEvent、wkeFireKeyDownEvent、wkeFireKeyPressEvent函数分别向wkeWebView发送键盘消息就可以了.于是我在对应的处理函数中添加了相关代码//OnChar unsigned int flags = 0; if (nFlags & KF_REPEAT) flags |= WKE_REPEAT; if (nFlags & KF_EXTENDED) flags |= WKE_EXTENDED; wkeFireKeyPressEvent(m_web, nChar, flags, false);//OnKeyUp unsigned int flags = 0; if (nFlags & KF_REPEAT) flags |= WKE_REPEAT; if (nFlags & KF_EXTENDED) flags |= WKE_EXTENDED; wkeFireKeyUpEvent(m_web, virtualKeyCode, flags, false);//OnKeyDown unsigned int flags = 0; if (nFlags & KF_REPEAT) flags |= WKE_REPEAT; if (nFlags & KF_EXTENDED) flags |= WKE_EXTENDED; wkeFireKeyDownEvent(m_web, virtualKeyCode, flags, false);但是这么干,我通过调试发现它好像并没有进入到这些函数里面来,也就是说键盘消息不是由主对话框来处理的。那么现在只能在wkeWebView 对应的窗口中来处理了。那么怎么捕获这个窗口的消息呢,miniblink提供了函数wkeGetHostHWND 来根据视图的句柄获取对应窗口的句柄,那么现在的思路就是这样的:首先获取对应的窗口句柄然后通过SetWindowLong来修改窗口的窗口过程,然后在窗口过程中处理这些消息就行了。根据这个思路整理一下代码//在创建wkeWebView 之后来hook窗口过程 HWND hWnd = wkeGetHostHWND(m_web); g_OldProc = (WNDPROC)SetWindowLong(hWnd, GWL_WNDPROC, (LONG)MyWndProc); //为了能够在全局函数中使用对话框类的东西,我们为窗口绑定一个对话框类的指针 SetWindowLong(hWnd, GWL_USERDATA, this);接着在MyWndProc中处理对应的消息事件LRESULT CALLBACK MyWndProc(HWND hWnd, UINT uMsg, WPARAM wParam, LPARAM lParam) { CWebBrowserDlg* pDlg = (CWebBrowserDlg*)GetWindowLong(hWnd, GWL_USERDATA); if (NULL == pDlg) { return CallWindowProc(g_OldProc, hWnd, uMsg, wParam, lParam); } switch (uMsg) { case WM_KEYUP: { unsigned int virtualKeyCode = wParam; unsigned int flags = 0; if (HIWORD(lParam) & KF_REPEAT) flags |= WKE_REPEAT; if (HIWORD(lParam) & KF_EXTENDED) flags |= WKE_EXTENDED; wkeFireKeyDownEvent(pDlg->m_web, virtualKeyCode, flags, false); } break; case WM_KEYDOWN: { unsigned int virtualKeyCode = wParam; unsigned int flags = 0; if (HIWORD(lParam) & KF_REPEAT) flags |= WKE_REPEAT; if (HIWORD(lParam) & KF_EXTENDED) flags |= WKE_EXTENDED; wkeFireKeyUpEvent(pDlg->m_web, virtualKeyCode, flags, false); } break; case WM_CHAR: { unsigned int charCode = wParam; unsigned int flags = 0; if (HIWORD(lParam) & KF_REPEAT) flags |= WKE_REPEAT; if (HIWORD(lParam) & KF_EXTENDED) flags |= WKE_EXTENDED; wkeFireKeyPressEvent(pDlg->m_web, charCode, flags, false); } break; default: return CallWindowProc(g_OldProc, hWnd, uMsg, wParam, lParam); } return 0; }这样做之后我发现它虽然能够截取到这些消息并执行它,但是在调用wkeFireKeyPressEvent等函数之后仍然无法响应键盘消息。难道是wkeCreateWebWindow 创建出来的窗口不能做子窗口?带着这个疑问我根据官方文档尝试了一下使用wkeCreateWebView ,然后将它绑定到对应的窗口上,然后这个整体作为子窗口的方式。代码太长了,我就不放出来了,有兴趣的可以翻到本文尾部,我将这个demo项目放到的GitHub上。结果还是不行。这些函数仍然进不来。真的郁闷,难道要换方案?我这个时候已经开始准备换方案了,在编译wke 的时候心情极度烦躁,我在之前的程序上不停的敲击键盘,就听见“等~等~等~”。我靠!这不是想从模态对话框上切换回主页面时的那个声音吗?会不会是因为模态对话框的关系?这个时候我瞬间来了灵感。那就换吧,主要改一下APP类中相关代码,吧模态改成非模态的就行CWebBrowserDlg *dlg = new CWebBrowserDlg(); dlg->Create(IDD_WEBBROWSER_DIALOG); m_pMainWnd = dlg; INT_PTR nResponse = dlg->ShowWindow(SW_SHOW); if (nResponse == IDOK) { // TODO: 在此放置处理何时用 // “确定”来关闭对话框的代码 } else if (nResponse == IDCANCEL) { // TODO: 在此放置处理何时用 // “取消”来关闭对话框的代码 } // 由于对话框已关闭,所以将返回 FALSE 以便退出应用程序, // 而不是启动应用程序的消息泵。 //由于是非模态对话框,所以这里需要自己写消息环 MSG msg = { 0 }; while (GetMessage(&msg, NULL, 0, 0)) { TranslateMessage(&msg); DispatchMessageW(&msg); } delete dlg;卧槽,居然成功了,能正常相应了!为什么模态就不行呢,后来我在复盘的时候想到,应该是wkeWebView的窗口并没有做成那种严格意义上的子窗口,它是一个独立的,所以模态对话框把消息给拦截了不让传到其他的窗口导致的这个问题。这个也算是成功了。这个时候问题又来了,程序关不掉了,虽然说窗口是关了,但是程序并没有退出,后来调试发现,消息环没有退出。这个时候我想到应该是关闭时调用的是EndDialog。但是此时已经改成非模态了,需要最后调用DestroyWindow,那么这个地方就得去对话框的OnClose消息中改。void CWebBrowserDlg::OnClose() { // TODO: 在此添加消息处理程序代码和/或调用默认值 DestroyWindow(); //CDialog::OnClose(); }好了,这个时候基本已经完成了。就剩下一些按钮事件处理了。按钮事件的处理这里直接贴代码吧,基本只有几行,很容易看懂的void CWebBrowserDlg::OnBnClickedBtnBack() { // TODO: 在此添加控件通知处理程序代码 if (wkeCanGoBack(m_web)) { wkeGoBack(m_web); } } void CWebBrowserDlg::OnBnClickedBtnForward() { // TODO: 在此添加控件通知处理程序代码 if (wkeCanGoForward(m_web)) { wkeGoForward(m_web); } } void CWebBrowserDlg::OnBnClickedBtnStop() { // TODO: 在此添加控件通知处理程序代码 wkeStopLoading(m_web); } void CWebBrowserDlg::OnBnClickedBtnRefresh() { // TODO: 在此添加控件通知处理程序代码 wkeReload(m_web); } void CWebBrowserDlg::OnBnClickedBtnGo() { // TODO: 在此添加控件通知处理程序代码 CString csurl; GetDlgItem(IDC_EDIT_URL)->GetWindowText(csurl); wkeLoadURLW(m_web, csurl); } //设置代理 void CWebBrowserDlg::OnBnClickedBtnProxy() { CDlgProxySet dlgProxySet; dlgProxySet.DoModal(); wkeProxy proxy; proxy.type = WKE_PROXY_HTTP; USES_CONVERSION; strcpy_s(proxy.hostname, sizeof(proxy.hostname), T2A(dlgProxySet.csIP)); proxy.port = dlgProxySet.m_port; wkeSetProxy(&proxy); // TODO: 在此添加控件通知处理程序代码 }wkeView 的回调函数现在主体功能已经完成了,要跟浏览器类似,需要处理这样几个东西。第一个是url栏中的内容会根据当前主页面的url做调整,特别是针对302、301 跳转的情况。第二个是窗口的标题应该改为页面的标题;第三个是在某些页面中超链接用的是_blank,时应该能正常打开新窗口。为了实现这些目标,我们需要处理一些wkeView的事件,我们创建了wkeWebView 之后直接绑定这些事件wkeOnTitleChanged(m_web, wkeOnTitleChangedCallBack, this); //最后一个参数是传递用户数据,这里我们传递this指针进去 wkeOnURLChanged(m_web, wkeOnURLChangedCallBack, this); wkeOnNavigation(m_web, wkeOnNavigationCallBack, this); wkeOnCreateView(m_web, onBrowserCreateView, this);// 页面标题更改时调用此回调 void _cdecl wkeOnTitleChangedCallBack(wkeWebView webView, void* param, const wkeString title) { CWebBrowserDlg *pDlg = (CWebBrowserDlg*)param; if (NULL != pDlg) { pDlg->SetWindowText(wkeGetStringW(title)); } } //url变更时调用此回调 void _cdecl wkeOnURLChangedCallBack(wkeWebView webView, void* param, const wkeString url) { CWebBrowserDlg *pDlg = (CWebBrowserDlg*)param; if (NULL != pDlg) { pDlg->GetDlgItem(IDC_EDIT_URL)->SetWindowTextW(wkeGetStringW(url)); } } //网页开始浏览将触发回调, 这里主要是为了它能打开一些本地的程序 bool _cdecl wkeOnNavigationCallBack(wkeWebView webView, void* param, wkeNavigationType navigationType, const wkeString url) { const wchar_t* urlStr = wkeGetStringW(url); if (wcsstr(urlStr, L"exec://") == urlStr) { PROCESS_INFORMATION processInfo = { 0 }; STARTUPINFOW startupInfo = { 0 }; startupInfo.cb = sizeof(startupInfo); BOOL succeeded = CreateProcessW(NULL, (LPWSTR)urlStr + 7, NULL, NULL, FALSE, 0, NULL, NULL, &startupInfo, &processInfo); if (succeeded) { CloseHandle(processInfo.hProcess); CloseHandle(processInfo.hThread); } return false; } return true; } //网页点击a标签创建新窗口时将触发回调 wkeWebView _cdecl onBrowserCreateView(wkeWebView webView, void* param, wkeNavigationType navType, const wkeString urlStr, const wkeWindowFeatures* features) { const wchar_t* url = wkeGetStringW(urlStr); wkeWebView newWindow = wkeCreateWebWindow(WKE_WINDOW_TYPE_POPUP, NULL, features->x, features->y, features->width, features->height); wkeShowWindow(newWindow, true); return newWindow; }至此这个浏览器的demo就完成了。最后贴上对应的demo项目地址: https://github.com/aMonst/WebBrowserPS:最近有一位朋友发邮件告诉我说,wkeWebView 不能响应键盘消息与对话框是模态还是非模态无关,主要是要处理wkeWebView的WM_GETDLGCODE 消息,那位朋友给出的代码如下:switch(uMsg) { case WM_GETDLGCODE: return DLGC_WANTARROWS | DLGC_WANTALLKEYS | DLGC_WANTCHARS; }我试了一下,发现确实是这样,相比较我上面提出的改为非模态的方式来说,还是用模态对话框方便、毕竟MFC对话框程序本来就是非模态的。所以这里我将代码做了一下修改。并同步到了GitHub上。最后再次感谢那位发邮件告诉的朋友。。。。。参考资料miniblink API文档官方DEMO -
 多结果集IMultipleResult接口 title: 多结果集IMultipleResult接口tags: [OLEDB, 数据库编程, VC++, 数据库]date: 2018-03-16 21:04:31categories: windows 数据库编程keywords: OLEDB, 数据库编程, VC++, 数据库, 结果集, 多结果集在某些任务中,需要执行多条sql语句,这样一次会返回多个结果集,在应用程序就需要处理多个结果集,在OLEDB中支持多结果集的接口是IMultipleResult。查询数据源是否支持多结果集并不是所有数据源都支持多结果集,可以通过查询数据源对象的DBPROPSET_DATASOURCEINFO属性集中的DBPROP_MULTIPLERESULTS属性来确定,该值是一个按位设置的4字节的联合值。它可取的值有下面几个:DBPROPVAL_MR_SUPPORITED:支持多结果集DBPROPVAL_MR_SONCURRENT:支持多结果集,并支持同时打开多个返回的结果集(如果它不支持同时打开多个结果集的话,在打开下一个结果集之前需要关闭已经打开的结果集)DBPROPVAL_MR_NOTSUPPORTED: 不支持多结果集这个属性可以通过接口IDBProperties接口的GetProperties方法来获取,该函数的原型如下:HRESULT GetProperties ( ULONG cPropertyIDSets, const DBPROPIDSET rgPropertyIDSets[], ULONG *pcPropertySets, DBPROPSET **prgPropertySets);它的用法与之前的SetProperties十分类似第一个参数是我们传入DBPROPIDSET数组元素的个数,第二个参数是一个DBPROPIDSET结构的参数,该结构的原型如下:typedef struct tagDBPROPIDSET { DBPROPID * rgPropertyIDs; ULONG cPropertyIDs; GUID guidPropertySet; } DBPROPIDSET;该结构与之前遇到的DBPROPSET类似,第一个参数是一个DBPROPID结构的数组的首地址,该值是一个属性值,表示我们希望查询哪个属性的情况,第二个参数表示我们总共查询多少个属性的值,第3个参数表示这些属性都属于哪个属性集。接口方法的第三个参数返回当前我们总共查询到几个属性集的内容。第四个参数返回具体查到的属性值。多结果集接口的使用多结果集对象的定义如下:CoType TMultipleResults { [mandatory] interface IMultipleResults; [optional] interface ISupportErrorInfo; }一般在程序中,使用多结果集有如下步骤查询数据源是否支持多结果集,如果不支持则要考虑其他的实现方案如果它支持多结果集,在调用ICommandText接口的Execute方法执行SQL语句时,让其返回一个IMultipleRowset接口。循环调用接口的GetResult方法获取结果集对象。使用结果集对象最后是一个完整的例子://判断是否支持多结果集 BOOL SupportMultipleRowsets(IOpenRowset *pIOpenRowset) { COM_DECLARE_BUFFER(); COM_DECLARE_INTERFACE(IDBInitialize); COM_DECLARE_INTERFACE(IDBProperties); COM_DECLARE_INTERFACE(IGetDataSource); BOOL bRet = FALSE; //定义相关结构用于获取关于多结果集的信息 DBPROPID dbPropId[2] = {0}; DBPROPIDSET dbPropIDSet[1] = {0}; dbPropId[0] = DBPROP_MULTIPLERESULTS; dbPropIDSet[0].cPropertyIDs = 1; dbPropIDSet[0].guidPropertySet = DBPROPSET_DATASOURCEINFO; dbPropIDSet[0].rgPropertyIDs = dbPropId; //定义相关结构用于接受返回的属性信息 ULONG uPropsets = 0; DBPROPSET *pDBPropset = NULL; //获取数据源对象 HRESULT hRes = pIOpenRowset->QueryInterface(IID_IGetDataSource, (void**)&pIGetDataSource); COM_SUCCESS(hRes, _T("查询接口IGetDataSource失败,错误码为:%08x\n"), hRes); hRes = pIGetDataSource->GetDataSource(IID_IDBInitialize, (IUnknown **)&pIDBInitialize); COM_SUCCESS(hRes, _T("获取数据源对象失败,错误码为:%08x\n"), hRes); //获取对应属性 hRes = pIDBInitialize->QueryInterface(IID_IDBProperties, (void**)&pIDBProperties); COM_SUCCESS(hRes, _T("查询IDBProperties接口失败,错误码为:%08x\n"), hRes); hRes = pIDBProperties->GetProperties(1, dbPropIDSet, &uPropsets, &pDBPropset); COM_SUCCESS(hRes, _T("获取属性信息失败,错误码:%08x\n"), hRes); //判断是否支持多结果集 if (pDBPropset[0].rgProperties[0].vValue.vt == VT_I4) { if (pDBPropset[0].rgProperties[0].vValue.intVal & DBPROPVAL_MR_CONCURRENT) { COM_PRINT(_T("支持多结果集\n")); }else if (pDBPropset[0].rgProperties[0].vValue.intVal & DBPROPVAL_MR_SUPPORTED) { COM_PRINT(_T("支持多结果集\n")); }else if (pDBPropset[0].rgProperties[0].vValue.intVal & DBPROPVAL_MR_NOTSUPPORTED) { COM_PRINT(_T("不支持多结果集\n")); goto __CLEAR_UP; } else { COM_PRINT(_T("未知\n")); goto __CLEAR_UP; } } bRet = TRUE; __CLEAR_UP: SAFE_RELSEASE(pIDBInitialize); SAFE_RELSEASE(pIDBProperties); SAFE_RELSEASE(pIGetDataSource); CoTaskMemFree(pDBPropset[0].rgProperties); CoTaskMemFree(pDBPropset); return bRet; } // 执行sql语句并返回多结果集对象 BOOL ExecSQL(LPOLESTR lpSQL, IOpenRowset *pIOpenRowset, IMultipleResults* &pIMultipleResults) { COM_DECLARE_BUFFER(); COM_DECLARE_INTERFACE(IDBCreateCommand); COM_DECLARE_INTERFACE(ICommandText); COM_DECLARE_INTERFACE(ICommandProperties); BOOL bRet = FALSE; DBPROP dbProp[2] = {0}; DBPROPSET dbPropset[1] = {0}; dbProp[0].colid = DB_NULLID; dbProp[0].dwOptions = DBPROPOPTIONS_REQUIRED; dbProp[0].dwPropertyID = DBPROP_UPDATABILITY; dbProp[0].vValue.vt = VT_I4; dbProp[0].vValue.intVal = DBPROPVAL_UP_CHANGE | DBPROPVAL_UP_DELETE | DBPROPVAL_UP_INSERT; //设置SQL语句 HRESULT hRes = pIOpenRowset->QueryInterface(IID_IDBCreateCommand, (void**)&pIDBCreateCommand); COM_SUCCESS(hRes, _T("查询接口IDBCreateCommand失败,错误码:%08x\n"), hRes); hRes = pIDBCreateCommand->CreateCommand(NULL , IID_ICommandText, (IUnknown**)&pICommandText); COM_SUCCESS(hRes, _T("创建接口ICommandText失败,错误码:%08x"), hRes); hRes = pICommandText->SetCommandText(DBGUID_DEFAULT, lpSQL); COM_SUCCESS(hRes, _T("设置SQL语句失败,错误码为:%08x\n"), hRes); //设置属性 hRes = pICommandText->QueryInterface(IID_ICommandProperties, (void**)&pICommandProperties); COM_SUCCESS(hRes, _T("查询接口ICommandProperties接口失败,错误码:%08x\n"), hRes); //执行SQL语句 hRes = pICommandText->Execute(NULL, IID_IMultipleResults, NULL, NULL, (IUnknown**)&pIMultipleResults); COM_SUCCESS(hRes, _T("执行SQL语句失败,错误码:%08x\n"), hRes); bRet = TRUE; __CLEAR_UP: SAFE_RELSEASE(pIDBCreateCommand); SAFE_RELSEASE(pICommandText); SAFE_RELSEASE(pICommandProperties); return bRet; } int _tmain(int argc, TCHAR *argv[]) { CoInitialize(NULL); COM_DECLARE_BUFFER(); COM_DECLARE_INTERFACE(IOpenRowset); COM_DECLARE_INTERFACE(IMultipleResults); COM_DECLARE_INTERFACE(IRowset); LPOLESTR pSQL = OLESTR("Select * From aa26 Where Left(aac031,2) = '11';\ Select * From aa26 Where Left(aac031,2) = '32';\ Select * From aa26 Where Left(aac031,2) = '21';"); if (!CreateSession(pIOpenRowset)) { goto __EXIT; } if (!SupportMultipleRowsets(pIOpenRowset)) { goto __EXIT; } if (!ExecSQL(pSQL, pIOpenRowset, pIMultipleResults)) { goto __EXIT; } //循环取结果集 while (TRUE) { HRESULT hr = pIMultipleResults->GetResult(NULL, DBRESULTFLAG_DEFAULT, IID_IRowset, NULL, (IUnknown**)&pIRowset); if (hr != S_OK) { break; } //后面的代码就是针对每个结果集来进行列的绑定与数据输出,在这就不列举出来了 __CLEAR_UP: CoTaskMemFree(pdbColumn); CoTaskMemFree(pColumsName); FREE(pDBBinding); FREE(pData); pIAccessor->ReleaseAccessor(hAccessor, NULL); SAFE_RELSEASE(pIColumnsInfo); SAFE_RELSEASE(pIAccessor); SAFE_RELSEASE(pIRowset); _tsystem(_T("PAUSE")); } __EXIT: SAFE_RELSEASE(pIOpenRowset); SAFE_RELSEASE(pIMultipleResults); CoUninitialize(); return 0; }最后贴出例子完整代码的链接:源代码查看
多结果集IMultipleResult接口 title: 多结果集IMultipleResult接口tags: [OLEDB, 数据库编程, VC++, 数据库]date: 2018-03-16 21:04:31categories: windows 数据库编程keywords: OLEDB, 数据库编程, VC++, 数据库, 结果集, 多结果集在某些任务中,需要执行多条sql语句,这样一次会返回多个结果集,在应用程序就需要处理多个结果集,在OLEDB中支持多结果集的接口是IMultipleResult。查询数据源是否支持多结果集并不是所有数据源都支持多结果集,可以通过查询数据源对象的DBPROPSET_DATASOURCEINFO属性集中的DBPROP_MULTIPLERESULTS属性来确定,该值是一个按位设置的4字节的联合值。它可取的值有下面几个:DBPROPVAL_MR_SUPPORITED:支持多结果集DBPROPVAL_MR_SONCURRENT:支持多结果集,并支持同时打开多个返回的结果集(如果它不支持同时打开多个结果集的话,在打开下一个结果集之前需要关闭已经打开的结果集)DBPROPVAL_MR_NOTSUPPORTED: 不支持多结果集这个属性可以通过接口IDBProperties接口的GetProperties方法来获取,该函数的原型如下:HRESULT GetProperties ( ULONG cPropertyIDSets, const DBPROPIDSET rgPropertyIDSets[], ULONG *pcPropertySets, DBPROPSET **prgPropertySets);它的用法与之前的SetProperties十分类似第一个参数是我们传入DBPROPIDSET数组元素的个数,第二个参数是一个DBPROPIDSET结构的参数,该结构的原型如下:typedef struct tagDBPROPIDSET { DBPROPID * rgPropertyIDs; ULONG cPropertyIDs; GUID guidPropertySet; } DBPROPIDSET;该结构与之前遇到的DBPROPSET类似,第一个参数是一个DBPROPID结构的数组的首地址,该值是一个属性值,表示我们希望查询哪个属性的情况,第二个参数表示我们总共查询多少个属性的值,第3个参数表示这些属性都属于哪个属性集。接口方法的第三个参数返回当前我们总共查询到几个属性集的内容。第四个参数返回具体查到的属性值。多结果集接口的使用多结果集对象的定义如下:CoType TMultipleResults { [mandatory] interface IMultipleResults; [optional] interface ISupportErrorInfo; }一般在程序中,使用多结果集有如下步骤查询数据源是否支持多结果集,如果不支持则要考虑其他的实现方案如果它支持多结果集,在调用ICommandText接口的Execute方法执行SQL语句时,让其返回一个IMultipleRowset接口。循环调用接口的GetResult方法获取结果集对象。使用结果集对象最后是一个完整的例子://判断是否支持多结果集 BOOL SupportMultipleRowsets(IOpenRowset *pIOpenRowset) { COM_DECLARE_BUFFER(); COM_DECLARE_INTERFACE(IDBInitialize); COM_DECLARE_INTERFACE(IDBProperties); COM_DECLARE_INTERFACE(IGetDataSource); BOOL bRet = FALSE; //定义相关结构用于获取关于多结果集的信息 DBPROPID dbPropId[2] = {0}; DBPROPIDSET dbPropIDSet[1] = {0}; dbPropId[0] = DBPROP_MULTIPLERESULTS; dbPropIDSet[0].cPropertyIDs = 1; dbPropIDSet[0].guidPropertySet = DBPROPSET_DATASOURCEINFO; dbPropIDSet[0].rgPropertyIDs = dbPropId; //定义相关结构用于接受返回的属性信息 ULONG uPropsets = 0; DBPROPSET *pDBPropset = NULL; //获取数据源对象 HRESULT hRes = pIOpenRowset->QueryInterface(IID_IGetDataSource, (void**)&pIGetDataSource); COM_SUCCESS(hRes, _T("查询接口IGetDataSource失败,错误码为:%08x\n"), hRes); hRes = pIGetDataSource->GetDataSource(IID_IDBInitialize, (IUnknown **)&pIDBInitialize); COM_SUCCESS(hRes, _T("获取数据源对象失败,错误码为:%08x\n"), hRes); //获取对应属性 hRes = pIDBInitialize->QueryInterface(IID_IDBProperties, (void**)&pIDBProperties); COM_SUCCESS(hRes, _T("查询IDBProperties接口失败,错误码为:%08x\n"), hRes); hRes = pIDBProperties->GetProperties(1, dbPropIDSet, &uPropsets, &pDBPropset); COM_SUCCESS(hRes, _T("获取属性信息失败,错误码:%08x\n"), hRes); //判断是否支持多结果集 if (pDBPropset[0].rgProperties[0].vValue.vt == VT_I4) { if (pDBPropset[0].rgProperties[0].vValue.intVal & DBPROPVAL_MR_CONCURRENT) { COM_PRINT(_T("支持多结果集\n")); }else if (pDBPropset[0].rgProperties[0].vValue.intVal & DBPROPVAL_MR_SUPPORTED) { COM_PRINT(_T("支持多结果集\n")); }else if (pDBPropset[0].rgProperties[0].vValue.intVal & DBPROPVAL_MR_NOTSUPPORTED) { COM_PRINT(_T("不支持多结果集\n")); goto __CLEAR_UP; } else { COM_PRINT(_T("未知\n")); goto __CLEAR_UP; } } bRet = TRUE; __CLEAR_UP: SAFE_RELSEASE(pIDBInitialize); SAFE_RELSEASE(pIDBProperties); SAFE_RELSEASE(pIGetDataSource); CoTaskMemFree(pDBPropset[0].rgProperties); CoTaskMemFree(pDBPropset); return bRet; } // 执行sql语句并返回多结果集对象 BOOL ExecSQL(LPOLESTR lpSQL, IOpenRowset *pIOpenRowset, IMultipleResults* &pIMultipleResults) { COM_DECLARE_BUFFER(); COM_DECLARE_INTERFACE(IDBCreateCommand); COM_DECLARE_INTERFACE(ICommandText); COM_DECLARE_INTERFACE(ICommandProperties); BOOL bRet = FALSE; DBPROP dbProp[2] = {0}; DBPROPSET dbPropset[1] = {0}; dbProp[0].colid = DB_NULLID; dbProp[0].dwOptions = DBPROPOPTIONS_REQUIRED; dbProp[0].dwPropertyID = DBPROP_UPDATABILITY; dbProp[0].vValue.vt = VT_I4; dbProp[0].vValue.intVal = DBPROPVAL_UP_CHANGE | DBPROPVAL_UP_DELETE | DBPROPVAL_UP_INSERT; //设置SQL语句 HRESULT hRes = pIOpenRowset->QueryInterface(IID_IDBCreateCommand, (void**)&pIDBCreateCommand); COM_SUCCESS(hRes, _T("查询接口IDBCreateCommand失败,错误码:%08x\n"), hRes); hRes = pIDBCreateCommand->CreateCommand(NULL , IID_ICommandText, (IUnknown**)&pICommandText); COM_SUCCESS(hRes, _T("创建接口ICommandText失败,错误码:%08x"), hRes); hRes = pICommandText->SetCommandText(DBGUID_DEFAULT, lpSQL); COM_SUCCESS(hRes, _T("设置SQL语句失败,错误码为:%08x\n"), hRes); //设置属性 hRes = pICommandText->QueryInterface(IID_ICommandProperties, (void**)&pICommandProperties); COM_SUCCESS(hRes, _T("查询接口ICommandProperties接口失败,错误码:%08x\n"), hRes); //执行SQL语句 hRes = pICommandText->Execute(NULL, IID_IMultipleResults, NULL, NULL, (IUnknown**)&pIMultipleResults); COM_SUCCESS(hRes, _T("执行SQL语句失败,错误码:%08x\n"), hRes); bRet = TRUE; __CLEAR_UP: SAFE_RELSEASE(pIDBCreateCommand); SAFE_RELSEASE(pICommandText); SAFE_RELSEASE(pICommandProperties); return bRet; } int _tmain(int argc, TCHAR *argv[]) { CoInitialize(NULL); COM_DECLARE_BUFFER(); COM_DECLARE_INTERFACE(IOpenRowset); COM_DECLARE_INTERFACE(IMultipleResults); COM_DECLARE_INTERFACE(IRowset); LPOLESTR pSQL = OLESTR("Select * From aa26 Where Left(aac031,2) = '11';\ Select * From aa26 Where Left(aac031,2) = '32';\ Select * From aa26 Where Left(aac031,2) = '21';"); if (!CreateSession(pIOpenRowset)) { goto __EXIT; } if (!SupportMultipleRowsets(pIOpenRowset)) { goto __EXIT; } if (!ExecSQL(pSQL, pIOpenRowset, pIMultipleResults)) { goto __EXIT; } //循环取结果集 while (TRUE) { HRESULT hr = pIMultipleResults->GetResult(NULL, DBRESULTFLAG_DEFAULT, IID_IRowset, NULL, (IUnknown**)&pIRowset); if (hr != S_OK) { break; } //后面的代码就是针对每个结果集来进行列的绑定与数据输出,在这就不列举出来了 __CLEAR_UP: CoTaskMemFree(pdbColumn); CoTaskMemFree(pColumsName); FREE(pDBBinding); FREE(pData); pIAccessor->ReleaseAccessor(hAccessor, NULL); SAFE_RELSEASE(pIColumnsInfo); SAFE_RELSEASE(pIAccessor); SAFE_RELSEASE(pIRowset); _tsystem(_T("PAUSE")); } __EXIT: SAFE_RELSEASE(pIOpenRowset); SAFE_RELSEASE(pIMultipleResults); CoUninitialize(); return 0; }最后贴出例子完整代码的链接:源代码查看 -
 算法与数据结构(四):树 前面说的链表、栈、队列都是线性结构,而树是一个非线性节点。树简介树是一种非线性结构,由一个根节点和若干个子节点构成,每一个子节点又是一颗子树从定义上来看树的定义是一个递归的定义,树都有一个根节点,其中当根节点为空时它也是一颗特殊的树,树的示意图如下:相关术语树的度:树中各节点中最大的子节点数就是树的度,没有子节点的节点称为叶子节点节点的层次:从根节点开始,根节点的子节点为1层,子节点的子节点为第二层,依次类推树的深度:组成树的各节点的最大层数父节点与孩子节点:若一个节点有子节点,那么这个节点称为子节点的父节点,它的子节点称为它的孩子节点兄弟节点:具有相同父节点的节点互称为兄弟节点节点的祖先:从根到该节点所经分支上的所有节点子孙:以某节点为根的子树中任一节点都称为该节点的子孙二叉树对于树来说,并没有规定它能拥有几个子节点。一般常用的是节点数小于等于2的树,这种树一般称为二叉树。二叉树一般有如下几种形式空二叉树, 根节点为空只有一个节点的二叉树,只有根节点的二叉树只有左子树的二叉树只有右子树的二叉树完全二叉树满二叉树完全二叉树:若设二叉树的深度为h,除第 h 层外,其它各层 (1~(h-1)层) 的结点数都达到最大个数,第h层所有的结点都连续集中在最左边,这就是完全二叉树。也就是说除了最深层的非叶子节点,每层的子节点都必须有两个子节点,而且最后一层少节点只能最右边少。满二叉树: 一颗深度为h的二叉树,它的节点如果有2^k - 1 的话,它就是一颗满二叉树。也就说满二叉树是除了叶子节点,每个节点都有两个子节点的树完全二叉树的性质:$$在第k层,最多只有 2^(k -1) 个节点$$$$深度为k的完全二叉树,最多有 2^k - 2 个节点$$$$具有n个节点的完全二叉树的深度为\lfloor log_2(n)\rfloor $$二叉树的创建从上面的定义来看,树是一个递归的定义,因此在创建它的时候采用的也是递归的方式。树的节点暂时定义为:typedef struct _BTREE { int nVal; struct _BTREE *pLeft; struct _BTREE *pRight; }BTREE, *LPBTREE;树的节点中有两个节点指针,分别指向左子树和右子树。LPBTREE CreateBTree() { int n = 0; scanf_s("%d", &n); if (0 == n) { return NULL; } //创建节点本身 BTREE *t = (BTREE*)malloc(sizeof(BTREE)); if (NULL == t) { return NULL; } memset(t, 0x00, sizeof(BTREE)); t->nVal = n; printf("请输入%d的左子节点:", n); //递归调用函数来创建它的左子树 t->pLeft = CreateBTree(); //递归调用来创建它的右子树 printf("请输入%d的右子节点:", n); t->pRight = CreateBTree(); return t; }树的遍历树的遍历一般有三种方式,先序遍历、中序遍历、后序遍历先序遍历是先遍历根节点,在遍历它的左子树,最后遍历右子树,针对每颗子树都采用这种方式中序遍历是先遍历左子树,再遍历根节点,最后遍历右子树,针对每颗子树都采取这种方式遍历后续遍历是先遍历左子树,再遍历右子树,最后遍历根节点,针对每颗子树都采用这种方式遍历假设现在有一颗二叉树如下所示采用先序遍历得到的结果是:a、b、d、h、i、e、c、f、j、g、k采用中序遍历得到的结果是:h、d、i、b、e、a、j、f、c、g、k采用后续遍历得到的结果是:h、i、d、e、b、j、f、k、g、c、a根据数的结构我们知道它的先序遍历、中序遍历、后序遍历。同样的根据先序遍历,中序遍历或者根据后序遍历中序遍历可以得到一棵树的结构从而得到它的另一种遍历方式。这里需要注意的是根据先序遍历和后序遍历是不能唯一确定一颗树的假设现在有一棵二叉树先序遍历为a、b、d、g、h、k、e、i、c、f、j,中序遍历为:g、d、h、k、b、e、i、a、c、f、j 可以推断出它的树结构并得到后续遍历的结果。根据先序遍历a为第一个元素,可以得知a为根节点,再根据中序遍历中a的位置可以知道,g、d、h、k、b、e、i 为a的左子树,c、f、j为a的右子树。而且b c分别是左子树和右子树的根节点先来分析a的做子树,在先序遍历中,第一个元素为b,而中序遍历中b的位置可以知道g、d、h、k为左子树而e、i为右子树,而且g e分别是左子树和右子树的根节点以此类推可以得到a的左子树的布局大致如下:树的遍历也是一个递归的过程,将每个子节点看做一颗完整的树,再次调用遍历函数。只是根据不同的遍历方式,遍历函数调用的时机不同罢了//先序遍历 void PreOrder(LPBTREE pRoot) { if (NULL == pRoot) { return; } //先遍历根节点 printf("%d ", pRoot->nVal); //遍历左子树 PreOrder(pRoot->pLeft); //遍历右子树 PreOrder(pRoot->pRight); }//中序遍历 void InOrder(LPBTREE pRoot) { if (NULL == pRoot) { return; } InOrder(pRoot->pLeft); printf("%d ", pRoot->nVal); InOrder(pRoot->pRight); }//后续遍历 void PostOrder(LPBTREE pRoot) { if (NULL == pRoot) { return; } PostOrder(pRoot->pLeft); PostOrder(pRoot->pRight); printf("%d ", pRoot->nVal); }其他二叉树在算法中,二叉树应用的最为广泛,根据不同的用途,又可以分为这么几类二叉排序树:所有的左子树的节点都小于根节点,所有右子树的节点都大于根节点,而树的左右子树本身又是一颗二叉排序树;对于二叉排序树来说,中序遍历可以得到一个有序的集合。对于同一组有序的数值,生成的二叉排序树并不是唯一的,一般树的深度越浅,查找效率越高平衡二叉树:平衡二叉树是对二叉排序树的一种改进,平衡二叉树左右子树的高度差不超过1,其平衡因子定义为其左子树与右子树高度的差值,为了保持这个状态,每当插入一个数据时都需要对整个树做大量的调整。
算法与数据结构(四):树 前面说的链表、栈、队列都是线性结构,而树是一个非线性节点。树简介树是一种非线性结构,由一个根节点和若干个子节点构成,每一个子节点又是一颗子树从定义上来看树的定义是一个递归的定义,树都有一个根节点,其中当根节点为空时它也是一颗特殊的树,树的示意图如下:相关术语树的度:树中各节点中最大的子节点数就是树的度,没有子节点的节点称为叶子节点节点的层次:从根节点开始,根节点的子节点为1层,子节点的子节点为第二层,依次类推树的深度:组成树的各节点的最大层数父节点与孩子节点:若一个节点有子节点,那么这个节点称为子节点的父节点,它的子节点称为它的孩子节点兄弟节点:具有相同父节点的节点互称为兄弟节点节点的祖先:从根到该节点所经分支上的所有节点子孙:以某节点为根的子树中任一节点都称为该节点的子孙二叉树对于树来说,并没有规定它能拥有几个子节点。一般常用的是节点数小于等于2的树,这种树一般称为二叉树。二叉树一般有如下几种形式空二叉树, 根节点为空只有一个节点的二叉树,只有根节点的二叉树只有左子树的二叉树只有右子树的二叉树完全二叉树满二叉树完全二叉树:若设二叉树的深度为h,除第 h 层外,其它各层 (1~(h-1)层) 的结点数都达到最大个数,第h层所有的结点都连续集中在最左边,这就是完全二叉树。也就是说除了最深层的非叶子节点,每层的子节点都必须有两个子节点,而且最后一层少节点只能最右边少。满二叉树: 一颗深度为h的二叉树,它的节点如果有2^k - 1 的话,它就是一颗满二叉树。也就说满二叉树是除了叶子节点,每个节点都有两个子节点的树完全二叉树的性质:$$在第k层,最多只有 2^(k -1) 个节点$$$$深度为k的完全二叉树,最多有 2^k - 2 个节点$$$$具有n个节点的完全二叉树的深度为\lfloor log_2(n)\rfloor $$二叉树的创建从上面的定义来看,树是一个递归的定义,因此在创建它的时候采用的也是递归的方式。树的节点暂时定义为:typedef struct _BTREE { int nVal; struct _BTREE *pLeft; struct _BTREE *pRight; }BTREE, *LPBTREE;树的节点中有两个节点指针,分别指向左子树和右子树。LPBTREE CreateBTree() { int n = 0; scanf_s("%d", &n); if (0 == n) { return NULL; } //创建节点本身 BTREE *t = (BTREE*)malloc(sizeof(BTREE)); if (NULL == t) { return NULL; } memset(t, 0x00, sizeof(BTREE)); t->nVal = n; printf("请输入%d的左子节点:", n); //递归调用函数来创建它的左子树 t->pLeft = CreateBTree(); //递归调用来创建它的右子树 printf("请输入%d的右子节点:", n); t->pRight = CreateBTree(); return t; }树的遍历树的遍历一般有三种方式,先序遍历、中序遍历、后序遍历先序遍历是先遍历根节点,在遍历它的左子树,最后遍历右子树,针对每颗子树都采用这种方式中序遍历是先遍历左子树,再遍历根节点,最后遍历右子树,针对每颗子树都采取这种方式遍历后续遍历是先遍历左子树,再遍历右子树,最后遍历根节点,针对每颗子树都采用这种方式遍历假设现在有一颗二叉树如下所示采用先序遍历得到的结果是:a、b、d、h、i、e、c、f、j、g、k采用中序遍历得到的结果是:h、d、i、b、e、a、j、f、c、g、k采用后续遍历得到的结果是:h、i、d、e、b、j、f、k、g、c、a根据数的结构我们知道它的先序遍历、中序遍历、后序遍历。同样的根据先序遍历,中序遍历或者根据后序遍历中序遍历可以得到一棵树的结构从而得到它的另一种遍历方式。这里需要注意的是根据先序遍历和后序遍历是不能唯一确定一颗树的假设现在有一棵二叉树先序遍历为a、b、d、g、h、k、e、i、c、f、j,中序遍历为:g、d、h、k、b、e、i、a、c、f、j 可以推断出它的树结构并得到后续遍历的结果。根据先序遍历a为第一个元素,可以得知a为根节点,再根据中序遍历中a的位置可以知道,g、d、h、k、b、e、i 为a的左子树,c、f、j为a的右子树。而且b c分别是左子树和右子树的根节点先来分析a的做子树,在先序遍历中,第一个元素为b,而中序遍历中b的位置可以知道g、d、h、k为左子树而e、i为右子树,而且g e分别是左子树和右子树的根节点以此类推可以得到a的左子树的布局大致如下:树的遍历也是一个递归的过程,将每个子节点看做一颗完整的树,再次调用遍历函数。只是根据不同的遍历方式,遍历函数调用的时机不同罢了//先序遍历 void PreOrder(LPBTREE pRoot) { if (NULL == pRoot) { return; } //先遍历根节点 printf("%d ", pRoot->nVal); //遍历左子树 PreOrder(pRoot->pLeft); //遍历右子树 PreOrder(pRoot->pRight); }//中序遍历 void InOrder(LPBTREE pRoot) { if (NULL == pRoot) { return; } InOrder(pRoot->pLeft); printf("%d ", pRoot->nVal); InOrder(pRoot->pRight); }//后续遍历 void PostOrder(LPBTREE pRoot) { if (NULL == pRoot) { return; } PostOrder(pRoot->pLeft); PostOrder(pRoot->pRight); printf("%d ", pRoot->nVal); }其他二叉树在算法中,二叉树应用的最为广泛,根据不同的用途,又可以分为这么几类二叉排序树:所有的左子树的节点都小于根节点,所有右子树的节点都大于根节点,而树的左右子树本身又是一颗二叉排序树;对于二叉排序树来说,中序遍历可以得到一个有序的集合。对于同一组有序的数值,生成的二叉排序树并不是唯一的,一般树的深度越浅,查找效率越高平衡二叉树:平衡二叉树是对二叉排序树的一种改进,平衡二叉树左右子树的高度差不超过1,其平衡因子定义为其左子树与右子树高度的差值,为了保持这个状态,每当插入一个数据时都需要对整个树做大量的调整。 -
 算法与数据结构(三):栈 栈与队列一样也是一种线性的数据结构,与队列不同的是栈是一种先进后出的结构,有点类似于现实中的弹夹,最后压进去的子弹总是最先被打出来,在计算机中栈用到的地方就是用作函数传参与函数中局部变量的保存,也就是我们经常说的函数栈。栈同样有基于数组和基于链表的实现基于链表的实现基于链表实现的栈只需要一个头指针即可,插入删除都在头部进行。基于链表的栈没有栈满这一说,栈空的条件是头指针为NULL。元素入栈bool Push(int nValue) { LPSTACK_NODE p = (LPSTACK_NODE)malloc(sizeof(STACK_NODE)); if (NULL == p) { return false; } memset(p, 0x00, sizeof(STACK_NODE)); p->nVal = nValue; p->pNext = g_Top; g_Top = p; return true; }参数入栈是不需要判断栈是否为空的,不管是否为空,我们都采用同样的算法,即先使新节点的next指针域指向头,然后再重新给头指针赋值,由于不涉及到头指针所指向地址的访问,所以不需要额外判断头指针是否为空元素出栈元素出栈首先需要判断栈是否为空,如果不为空,则需要一个临时指针保存出栈元素,然后将头指针进行偏移bool Pop(int* pValue) { if (NULL == pValue) { return false; } if (IsStackEmpty()) { return false; } *pValue = g_Top->nVal; LPSTACK_NODE p = g_Top; g_Top = g_Top->pNext; free(p); return true; }基于数组实现的栈基于数组实现的栈也需要一个指针(或者在这里称之为下标),指向栈顶,在函数栈中这个充当栈顶指针的是一个寄存器ESP,而在函数栈中还有一个栈的基地址是ebp,基于数组的栈中,这个基地址就是数组的首地址。在基于数组实现的栈中,根据栈顶指针是否为0来判断。另外这种栈需要判断栈是否已满,一般采用的判断方式是判断栈顶指针是否为数组的最大长度。栈空、栈满判断bool IsStackEmpty() { return g_Top == 0; } bool IsStackFull() { return g_Top == MAX_SIZE; }根据不同的实现方式会有不同的判断方式,这里是让栈顶指针指向下一个即将入栈的元素所在的位置,如果栈顶指针指向的是当前栈顶元素的位置,那么这里可能需要改为 等于 -1来判断栈空,等于MAX_SIZE - 1来判断栈满元素入栈bool Push(int nValue) { if (IsStackFull()) { return false; } g_STACK[g_Top++] = nValue; return true; }元素出栈bool Pop(int* pValue) { if (NULL == pValue) { return false; } if (IsStackEmpty()) { return false; } *pValue = g_STACK[--g_Top]; return true; }由于栈都是在一端进行操作,所以不存在向队列那样有空间浪费,也不需要实现什么循环数组。从实现上来看栈比队列要简单的多。
算法与数据结构(三):栈 栈与队列一样也是一种线性的数据结构,与队列不同的是栈是一种先进后出的结构,有点类似于现实中的弹夹,最后压进去的子弹总是最先被打出来,在计算机中栈用到的地方就是用作函数传参与函数中局部变量的保存,也就是我们经常说的函数栈。栈同样有基于数组和基于链表的实现基于链表的实现基于链表实现的栈只需要一个头指针即可,插入删除都在头部进行。基于链表的栈没有栈满这一说,栈空的条件是头指针为NULL。元素入栈bool Push(int nValue) { LPSTACK_NODE p = (LPSTACK_NODE)malloc(sizeof(STACK_NODE)); if (NULL == p) { return false; } memset(p, 0x00, sizeof(STACK_NODE)); p->nVal = nValue; p->pNext = g_Top; g_Top = p; return true; }参数入栈是不需要判断栈是否为空的,不管是否为空,我们都采用同样的算法,即先使新节点的next指针域指向头,然后再重新给头指针赋值,由于不涉及到头指针所指向地址的访问,所以不需要额外判断头指针是否为空元素出栈元素出栈首先需要判断栈是否为空,如果不为空,则需要一个临时指针保存出栈元素,然后将头指针进行偏移bool Pop(int* pValue) { if (NULL == pValue) { return false; } if (IsStackEmpty()) { return false; } *pValue = g_Top->nVal; LPSTACK_NODE p = g_Top; g_Top = g_Top->pNext; free(p); return true; }基于数组实现的栈基于数组实现的栈也需要一个指针(或者在这里称之为下标),指向栈顶,在函数栈中这个充当栈顶指针的是一个寄存器ESP,而在函数栈中还有一个栈的基地址是ebp,基于数组的栈中,这个基地址就是数组的首地址。在基于数组实现的栈中,根据栈顶指针是否为0来判断。另外这种栈需要判断栈是否已满,一般采用的判断方式是判断栈顶指针是否为数组的最大长度。栈空、栈满判断bool IsStackEmpty() { return g_Top == 0; } bool IsStackFull() { return g_Top == MAX_SIZE; }根据不同的实现方式会有不同的判断方式,这里是让栈顶指针指向下一个即将入栈的元素所在的位置,如果栈顶指针指向的是当前栈顶元素的位置,那么这里可能需要改为 等于 -1来判断栈空,等于MAX_SIZE - 1来判断栈满元素入栈bool Push(int nValue) { if (IsStackFull()) { return false; } g_STACK[g_Top++] = nValue; return true; }元素出栈bool Pop(int* pValue) { if (NULL == pValue) { return false; } if (IsStackEmpty()) { return false; } *pValue = g_STACK[--g_Top]; return true; }由于栈都是在一端进行操作,所以不存在向队列那样有空间浪费,也不需要实现什么循环数组。从实现上来看栈比队列要简单的多。 -
 算法与数据结构(二):队列 队列也是一种线性的数据结构,它与链表的区别在于链表可以在任意位置进行插入删除操作,而队列只能在一端进行插入,另一端进行删除。它对应于现实世界中的排队模型。队列有两种常见的实现方式:基于列表的实现和基于数组的实现基于链表的实现基于链表的队列,我们需要保存两个指针,一个指向头节点,一个指向尾节点。这种队列不存在队列满的情况,当然也可以根据业务需求给定一个最大值。当头结点为空时表示队列为空。由于队列只能在队尾插入数据,队首删除数据,因此针对队列的插入需要采用链表的尾插法,队列元素的出队需要改变头指针。队列节点的定义与链表节点的定义相同,下面给出各种操作的简单实现typedef struct _QNODE { int nValue; struct _QNODE *pNext; }QNODE, *LPQNODE; extern QNODE* g_front; extern QNODE* g_real;初始化初始化操作,我们简单的对两个指针进行赋值bool InitQueue() { g_front = g_real = NULL; return true; }元素入队元素入队的操作就是从队列尾部插入,当队列为空时,同时也是在队首插入元素,因此针对元素入队的操作,需要首先判断队列是否为空,为空时,需要针对队首和队尾指针进行赋值,而针对队列不为空的情况下,只需要改变队尾指针bool EnQueue(int nVal) { QNODE *p = (QNODE*)malloc(sizeof(QNO if (NULL == p) { return false; } memset(p, 0x00, sizeof(QNODE)); p->nValue = nVal; if (IsQueueEmpty()) //判断队列是否为空 { g_front = g_real = p; }else { g_real->pNext = p; g_real = p; } return true; }判断队列是否为空之前提到过,判断队列是否为空,只需要判断两个指针是否为空即可,因此这部分的代码如下:bool IsQueueEmpty() { return (g_front == NULL && g_real == NULL); }元素出队元素出队需要从队首出队,同样的需要判断队列是否为空。bool DeQueue(int *pVal) { if(NULL == pVal) { return false; } if (IsQueueEmpty()) { return false; } QNODE *p = g_front; //出队之后需要判断队列是否为空,以便针对队首、队尾指针进行赋值 if (NULL == g_front->pNext) { *pVal = g_front->nValue; g_front = NULL; g_real = NULL; }else { *pVal = g_front->nValue; g_front = g_front->pNext; } free(p); return true; } 基于数组的实现线性结构的队列也可以使用数组来实现,基于数组的实现也需要两个指针,分别是指向头部的下标和指向尾部的下标基于数组的实现中有这样一个问题,那就是内存资源的浪费问题。假设现在有一个能存储10个元素的队列,当前队列为空,随着元素的入队,此时队尾指针会一直向后偏移。当里面有部分元素的时候,来进行元素出队,这个时候队首指针会向后偏移。那么这个时候已经出队的位置在队列中再也访问不到了,但是它所占的内存仍然在那,这样就造成了内存空间的浪费,随着队列的不断使用,队列所能容纳的元素总数会不断减少。如图所示基于这种问题,我们采用循环数组的形式来表示一个队列,循环数组的结构大致如下图所示:这种队列的头指针不一定小于尾指针,当队首元素元素位于数组的尾部,这个时候只要数组中仍然有空闲位置来存储数据的时候,可以将队首指针再次指向数组的头部,从而实现空间的重复利用.在这种情况下队列的头部指针的计算公式为: head = (head + 1) % MAXSIZE,尾部的计算公式为 tail = (tail + 1) % MAXSIZE当队列为空时应该是 head == tail,注意,由于数组是循环数组,此时并不一定能保证它们二者都为0,只有当队列中从来没有过数据,也就是说是刚刚初始化完成的时候它们才都为0那么队列为满的情况又怎么确定呢?在使用普通数组的时候,当二者相等都为MAXSIZE的时候队列为满,但是在循环队列中,并不能根据二者都等于MAXSIZE来判断队列是否已满,有可能之前进行过出队的操作,所以在队列头之前的位置仍然能存数据,所以不能根据这个条件判断。那么是不是可以根据二者相等来判断呢?答案是不能,二者相等是用来判断队列为空的,那么怎么判断呢?这时候需要空出一块位置作为队尾的结束标志,回想一下给出的循环数组的实例图,每当head与tail只间隔一个元素的时候作为队列已满的标识。这个时候判断的公式为 (tail + 1) % MAXSIZE == head下面给出各种操作对应的代码队列的初始化int g_Queue[MAX_SIZE] = {0}; int g_front = 0; int g_real = 0; bool InitQueue() { g_front = g_real = 0; memset(g_Queue, 0x00, sizeof(g_Queue)); return true; } 入队bool EnQueue(int nVal) { if (IsQueueFull()) { return false; } g_Queue[g_real] = nVal; g_real = (g_real + 1) % MAX_SIZE; return true; }出队bool DeQueue(int *pVal) { if (NULL == pVal) { return false; } if (IsQueueFull()) { return false; } *pVal = g_Queue[g_front]; g_front = (g_front + 1) % MAX_SIZE; return true; }判断队空与队满bool IsQueueEmpty() { return g_real == g_front; } bool IsQueueFull() { return (( g_real + 1 ) % MAX_SIZE) == g_front; }最后从实现上来看基于数组的队列要比基于链表的简单许多,不需要考虑空指针,内存分配的问题,但是基于数组的队列需要额外考虑是否已满的情况,当然这个问题可以使用动态数组来避免。
算法与数据结构(二):队列 队列也是一种线性的数据结构,它与链表的区别在于链表可以在任意位置进行插入删除操作,而队列只能在一端进行插入,另一端进行删除。它对应于现实世界中的排队模型。队列有两种常见的实现方式:基于列表的实现和基于数组的实现基于链表的实现基于链表的队列,我们需要保存两个指针,一个指向头节点,一个指向尾节点。这种队列不存在队列满的情况,当然也可以根据业务需求给定一个最大值。当头结点为空时表示队列为空。由于队列只能在队尾插入数据,队首删除数据,因此针对队列的插入需要采用链表的尾插法,队列元素的出队需要改变头指针。队列节点的定义与链表节点的定义相同,下面给出各种操作的简单实现typedef struct _QNODE { int nValue; struct _QNODE *pNext; }QNODE, *LPQNODE; extern QNODE* g_front; extern QNODE* g_real;初始化初始化操作,我们简单的对两个指针进行赋值bool InitQueue() { g_front = g_real = NULL; return true; }元素入队元素入队的操作就是从队列尾部插入,当队列为空时,同时也是在队首插入元素,因此针对元素入队的操作,需要首先判断队列是否为空,为空时,需要针对队首和队尾指针进行赋值,而针对队列不为空的情况下,只需要改变队尾指针bool EnQueue(int nVal) { QNODE *p = (QNODE*)malloc(sizeof(QNO if (NULL == p) { return false; } memset(p, 0x00, sizeof(QNODE)); p->nValue = nVal; if (IsQueueEmpty()) //判断队列是否为空 { g_front = g_real = p; }else { g_real->pNext = p; g_real = p; } return true; }判断队列是否为空之前提到过,判断队列是否为空,只需要判断两个指针是否为空即可,因此这部分的代码如下:bool IsQueueEmpty() { return (g_front == NULL && g_real == NULL); }元素出队元素出队需要从队首出队,同样的需要判断队列是否为空。bool DeQueue(int *pVal) { if(NULL == pVal) { return false; } if (IsQueueEmpty()) { return false; } QNODE *p = g_front; //出队之后需要判断队列是否为空,以便针对队首、队尾指针进行赋值 if (NULL == g_front->pNext) { *pVal = g_front->nValue; g_front = NULL; g_real = NULL; }else { *pVal = g_front->nValue; g_front = g_front->pNext; } free(p); return true; } 基于数组的实现线性结构的队列也可以使用数组来实现,基于数组的实现也需要两个指针,分别是指向头部的下标和指向尾部的下标基于数组的实现中有这样一个问题,那就是内存资源的浪费问题。假设现在有一个能存储10个元素的队列,当前队列为空,随着元素的入队,此时队尾指针会一直向后偏移。当里面有部分元素的时候,来进行元素出队,这个时候队首指针会向后偏移。那么这个时候已经出队的位置在队列中再也访问不到了,但是它所占的内存仍然在那,这样就造成了内存空间的浪费,随着队列的不断使用,队列所能容纳的元素总数会不断减少。如图所示基于这种问题,我们采用循环数组的形式来表示一个队列,循环数组的结构大致如下图所示:这种队列的头指针不一定小于尾指针,当队首元素元素位于数组的尾部,这个时候只要数组中仍然有空闲位置来存储数据的时候,可以将队首指针再次指向数组的头部,从而实现空间的重复利用.在这种情况下队列的头部指针的计算公式为: head = (head + 1) % MAXSIZE,尾部的计算公式为 tail = (tail + 1) % MAXSIZE当队列为空时应该是 head == tail,注意,由于数组是循环数组,此时并不一定能保证它们二者都为0,只有当队列中从来没有过数据,也就是说是刚刚初始化完成的时候它们才都为0那么队列为满的情况又怎么确定呢?在使用普通数组的时候,当二者相等都为MAXSIZE的时候队列为满,但是在循环队列中,并不能根据二者都等于MAXSIZE来判断队列是否已满,有可能之前进行过出队的操作,所以在队列头之前的位置仍然能存数据,所以不能根据这个条件判断。那么是不是可以根据二者相等来判断呢?答案是不能,二者相等是用来判断队列为空的,那么怎么判断呢?这时候需要空出一块位置作为队尾的结束标志,回想一下给出的循环数组的实例图,每当head与tail只间隔一个元素的时候作为队列已满的标识。这个时候判断的公式为 (tail + 1) % MAXSIZE == head下面给出各种操作对应的代码队列的初始化int g_Queue[MAX_SIZE] = {0}; int g_front = 0; int g_real = 0; bool InitQueue() { g_front = g_real = 0; memset(g_Queue, 0x00, sizeof(g_Queue)); return true; } 入队bool EnQueue(int nVal) { if (IsQueueFull()) { return false; } g_Queue[g_real] = nVal; g_real = (g_real + 1) % MAX_SIZE; return true; }出队bool DeQueue(int *pVal) { if (NULL == pVal) { return false; } if (IsQueueFull()) { return false; } *pVal = g_Queue[g_front]; g_front = (g_front + 1) % MAX_SIZE; return true; }判断队空与队满bool IsQueueEmpty() { return g_real == g_front; } bool IsQueueFull() { return (( g_real + 1 ) % MAX_SIZE) == g_front; }最后从实现上来看基于数组的队列要比基于链表的简单许多,不需要考虑空指针,内存分配的问题,但是基于数组的队列需要额外考虑是否已满的情况,当然这个问题可以使用动态数组来避免。 -
 算法与数据结构(二):链表 上一篇简单的开了一个头,简单介绍了一下所谓的时间复杂度与空间复杂度,从这篇开始将陆陆续续写一下常用的数据结构:链表、队列、栈、树等等。链表当初是我在学校时唯一死磕过的数据结构,那个时候自己还算是一个好学生,虽然上课没怎么听懂,但是课后还是根据仔细调试过老师给的代码,硬是自己给弄懂了,它是我离校时唯一能够写出实现的数据结构,现在回想起来应该是它比较简单,算法也比较直来直去吧。虽然它比较简单,很多朋友也都会链表。但是作为一个系列,如果仅仅因为它比较简单而不去理会,总觉得少了点什么,所以再这仍然将其列举出来。单向链表单向链表是链表中的一种,它的特点是只有一个指向下一个节点的指针域,对单向链表的访问需要从头部开始,根据指针域依次访问下一个节点,单向链表的结构如下图所示单向链表的创建单向链表的结构只需要一个数据域与指针域,这个数据域可以是一个结构体,也可以是多个基本数据类型;指针域是一个指向节点类型的指针,简单的定义如下:typedef struct _LIST_NODE { int nVal; struct _LIST_NODE *pNext; }LIST_NODE, *LPLIST_NODE;创建链表可以采用头插法或者尾插法来初始化一个有多个节点的链表头插法的示意图如下:它的过程就像示意图中展现的,首先使用新节点p的next指针指向当前的头节点把新节点加入到链表头,然后变更链表头指针,这样就在头部插入了一个节点,用代码来展示就是p->next = head; head = p;我们使用一个函数来封装就是LPLIST_NODE CreateListHead() { LPLIST_NODE pHead = NULL; while (TRUE) { LPLIST_NODE p = (LPLIST_NODE)malloc(sizeof(LIST_NODE)); if (NULL == p) { break; } memset(p, 0x00, sizeof(LIST_NODE)); printf("请输入节点值(为0时将退出创建节点):"); scanf_s("%d", &p->nVal); //这里不需要对链表为空单独讨论 //当链表为空时pHead 的值为NULL, 这两句代码就变为 //p->pNext = NULL; //pHead = p; p->pNext = pHead; pHead = p; if (p->nVal == 0) { break; } } return pHead; }采用尾插法的话,首先得获得链表的尾部 pTail, 然后使尾节点的next指针指向新节点,然后更新尾节点,用代码来表示就是pTail->next = p; pTail = p;下面的函数是采用尾插法来构建链表的例子//这个函数多定义了一个变量用来保存 // 可以不需要这个变量,这样在插入之前需要遍历一遍链表,以便找到尾节点 // 但是每次插入之前都需要遍历一遍,没有定义一个变量保存尾节点这种方式来的高效 LPLIST_NODE CreateListTail() { LPLIST_NODE pHead = NULL; LPLIST_NODE pTail = pHead; while (NULL != pTail && NULL != pTail->pNext) { pTail = pTail->pNext; } while (TRUE) { LPLIST_NODE p = (LPLIST_NODE)malloc(sizeof(LIST_NODE)); if (NULL == p) { break; } memset(p, 0x00, sizeof(LIST_NODE)); printf("请输入节点值(为0时将退出创建节点):"); scanf_s("%d", &p->nVal); //由于这种方法需要对尾节点的next域赋值,所以需要考虑链表为空的情况 if (NULL == pTail) { pHead = p; pTail = pHead; }else { pTail->pNext = p; pTail = p; } if (p->nVal == 0) { break; } } return pHead; }链表的遍历链表的每个节点在内存中不是连续的,所以它不能像数组那样根据下标来访问(当然可以利用C++中的运算符重载来实现使用下标访问),链表中的每一个节点都保存了下一个节点的地址,所以我们根据每个节点指向的下一个节点来依次访问每个节点,访问的代码如下:void TraverseList(LPLIST_NODE pHead) { while (NULL != pHead) { printf("%d\n", pHead->nVal); pHead = pHead->pNext; } }链表的删除链表的每个节点都是在堆上分配的,在不再使用的时候需要手工清除每个节点。清除时需要使用遍历的方法,一个个的删除,只是需要在遍历的指针移动到下一个节点前保存当前节点,以便能够删除当前节点,删除的函数如下void DestroyList(LPLIST_NODE pHead) { LPLIST_NODE pTmp = pHead; while (NULL != pTmp) { pTmp = pHead->pNext; delete pHead; pHead = pTmp; } }删除单个节点如上图所示,假设我们要删除q节点,那么首先需要遍历找到q的上一个节点p,将p的next指针指向q的下一个节点,也就是赋值为q的next指针的值,用代码表示就是p->next = q->next;删除节点的函数如下:void DeleteNode(LPLIST_NODE* ppHead, int nValue) { if (NULL == ppHead || NULL == *ppHead) { return; } LPLIST_NODE p, q; p = *ppHead; while (NULL != p) { if (nValue == p->nVal) { if (*ppHead == p) { *ppHead = p->pNext; free(p); }else { q->pNext = p->pNext; free(p); } p = NULL; q = NULL; break; } q = p; p = p->pNext; } }在上述代码中首先来遍历链表,找到要删除的节点p和它的上一个节点q,由于头节点没有上一个节点,所以需要特别判断一下需要删除的是否为头节点,如果为头结点,则直接将头指针指向它的下一个节点,然后删除头结点即可,如果不是则采用之前的方法来删除。任意位置插入节点如上图所示,如果需要在q节点之后插入p节点的话,需要两步,将q的next节点指向q,然后将q指向之前p的下一个节点,这个时候需要注意一下顺序,如果我们先执行q->next = p 的话,那么之前q的下一个节点的地址就被覆盖掉了,这个时候后面的节点都丢掉了,所以这里我们要先执行p->next = q->next 这条语句,然后在执行q->next = p下面是一个创建有序链表的例子,这个例子演示了在任意位置插入节点LPLIST_NODE CreateSortedList() { LPLIST_NODE pHead = NULL; while (TRUE) { LPLIST_NODE p = (LPLIST_NODE)malloc(sizeof(LIST_NODE)); if (NULL == p) { break; } memset(p, 0x00, sizeof(LIST_NODE)); printf("请输入节点值(为0时将退出创建节点):"); scanf_s("%d", &p->nVal); if (NULL == pHead) { pHead = p; }else { if (pHead->nVal > p->nVal) { p->pNext = pHead; pHead = p; }else { LPLIST_NODE q = pHead; LPLIST_NODE r = q; q = q->pNext; while (NULL != q && q->nVal < p->nVal) { r = q; q = q->pNext; } p->pNext = r->pNext; r->pNext = p; } } if (p->nVal == 0) { break; } } return pHead; }当确定新节点的值之后,首先遍历链表,直到找到比新节点中数值大的节点,那么这个新节点就是需要插入到该节点之前。在遍历的时候使用r来保存之前的节点。这里需要注意这些情况:链表为空:这种情况下,直接让头指针指向当前节点如果头节点本身就是大于新节点的值,这种情况下采用头插法,将新节点插入到头部如果链表中未找到比新节点的值更大的值,这种情况下直接采用尾插发在链表中找到比新节点值更大的节点,这种情况下,在链表中插入但是在代码中并没有考虑到尾部插入的情况,由于在尾部插入时,r等于尾节点,r->pNext 的值为NULL, 所以 p->pNext = r->pNext;r->pNext = p; 可以看成 p->pNext = NULL; r->pNext = p; 也就是将p的next指针指向空,让其作为尾节点,将之前的尾节点的next指针指向新节点。循环链表循环链表是建立在单向链表的基础之上的,循环链表的尾节点并不指向空,而是指向其他的节点,可以是头结点,可以是自身,也可以是链表中的其他节点,为了方便操作,一般将循环链表的尾节点的next指针指向头节点,它的操作与单链表的操作类似,只需要将之前判断尾节点的条件变为 pTail->pNext == pHead 即可。这里就不再详细分析每种操作了,直接给出代码LPLIST_NODE CreateLoopList() { LPLIST_NODE pHead = NULL; LPLIST_NODE pTail = pHead; while(1) { LPLIST_NODE p = (LPLIST_NODE)malloc(sizeof(LIST_NODE)); if (NULL == p) { break; } memset(p, 0x00, sizeof(LIST_NODE)); printf("请输入一个值:"); scanf_s("%d", &p->nVal); if (NULL == pHead) { pHead = p; p->pNext = pHead; pTail = pHead; }else { pTail->pNext = p; p->pNext = pHead; pTail = p; } if (0 == p->nVal) { break; } } return pHead; } void TraverseLoopList(LPLIST_NODE pHead) { LPLIST_NODE pTmp = pHead; if (NULL == pTmp) { return; } do { printf("%d, ", pTmp->nVal); pTmp = pTmp->pNext; } while (pTmp != pHead); } void DestroyLoopList(LPLIST_NODE pHead) { LPLIST_NODE pTmp = pHead; LPLIST_NODE pDestroy = pTmp; if (NULL == pTmp) { return; } do { pTmp = pDestroy->pNext; free(pDestroy); pDestroy = pTmp; }while (pHead != pTmp); }判断链表是否为循环链表在上面说过,循环链表的尾指针不一定指向头节点,它可以指向任何节点,那么该怎么判断一个节点是否为循环链表呢?既然它可以指向任意的节点,那么肯定是找不到尾节点的,而且堆内存的分配是随机的,我们也不可能按照指针变量的大小来判断哪个节点在前哪个在后。回想一下在学校跑一千米的时候是不是回出现这样的情况,跑的块的会领先跑的慢的一周?根据这种情形我们可以考虑使用这样一种办法:定义两个指针,一个一次走两步也是就是p = p->next->next, 一个慢指针一次走一步,也就是q = q->next,如果是循环链表,那么快指针在某个时候一定会领先慢指针一周,也就是达到 p == q 这个条件,否则就是非循环链表。根据这个思路,可以考虑写下如下代码:bool IsLoopList(LPLIST_NODE pHead) { if (NULL == pHead) { return false; } LPLIST_NODE p = pHead; LPLIST_NODE q = pHead->pNext; while (NULL != p && NULL != q && NULL != q->pNext && p != q) { p = p->pNext; q = q->pNext->pNext; } if (q == NULL || NULL == p || NULL == q->pNext) { return false; } return true; }双向链表之前在插入或者删除的时候,需要定义两个指针变量,让其中一个一直更在另一个的后面,单向链表有一个很大的问题,不能很方便的找到它的上一个节点,为了解决这一个问题,提出了双向链表,双向链表与单向相比,多了一个指针域,用来指向它的上一个节点,也就是如下图所示:双向链表的操作与单向链表的类似,只是多了一个指向前一个节点的指针域,它要考虑的情况与单向链表相似删除节点删除节点的示意图如下:假设删除的节点p,那么首先根据p的pre指针域,找到它的上一个节点q,采用与单向链表类似的操作:q->next = p->next; p->next->pre = q;下面是删除节点的例子:void DeleteDNode(LPDLIST_NODE* ppHead, int nValue) { if (NULL == ppHead || NULL == *ppHead) { return; } LPDLIST_NODE p = *ppHead; while (NULL != p && p->nVal != nValue) { p = p->pNext; } if (NULL == p) { return; } if (*ppHead == p) { *ppHead = (*ppHead)->pNext; p->pPre = NULL; free(p); } else if (p->pNext == NULL) { p->pPre->pNext = NULL; free(p); }else { p->pPre->pNext = p->pNext; p->pNext->pPre = p->pPre; } }插入节点插入节点的示意图如下:假设新节点为p,插入的位置为q,则插入操作可以进行如下操作p->next = q->next; p->pre = q; q->next->pre = p; q->next = p;也是一样要考虑不能覆盖q的next指针域否则可能存在找不到原来链表中q的下一个节点的情况。所以这里先对p的next指针域进行操作下面也是采用创建有序列表的例子LPDLIST_NODE CreateSortedDList() { LPDLIST_NODE pHead = NULL; while (1) { LPDLIST_NODE pNode = (LPDLIST_NODE)malloc(sizeof(DLIST_NODE)); if (NULL == pNode) { return pHead; } memset(pNode, 0x00, sizeof(DLIST_NODE)); printf("请输入一个整数:"); scanf_s("%d", &pNode->nVal); if(NULL == pHead) { pHead = pNode; }else { LPDLIST_NODE q = pHead; LPDLIST_NODE r = q; while (NULL != q && q->nVal < pNode->nVal) { r = q; q = q->pNext; } if (q == pHead) { pNode->pNext = pHead; pHead->pPre = pNode; pHead = pNode; }else if (NULL == q) { r->pNext = pNode; pNode->pPre = r; }else { pNode->pPre = r; pNode->pNext = q; r->pNext = pNode; q->pPre = pNode; } } LPDLIST_NODE q = pHead; LPDLIST_NODE r = q; if (0 == pNode->nVal) { break; } } return pHead; }链表还有一种是双向循环链表,对于这种链表主要是在双向链表的基础上,将头结点的pre指针指向某个节点,将尾节点的next节点指向某个节点,而且这两个指针可以指向同一个节点也可以指向不同的节点,一般在使用中都是head的pre节点指向尾节点,而tail的next节点指向头节点。这里就不再详细说明,这些链表只要掌握其中一种,剩下的很好掌握的。
算法与数据结构(二):链表 上一篇简单的开了一个头,简单介绍了一下所谓的时间复杂度与空间复杂度,从这篇开始将陆陆续续写一下常用的数据结构:链表、队列、栈、树等等。链表当初是我在学校时唯一死磕过的数据结构,那个时候自己还算是一个好学生,虽然上课没怎么听懂,但是课后还是根据仔细调试过老师给的代码,硬是自己给弄懂了,它是我离校时唯一能够写出实现的数据结构,现在回想起来应该是它比较简单,算法也比较直来直去吧。虽然它比较简单,很多朋友也都会链表。但是作为一个系列,如果仅仅因为它比较简单而不去理会,总觉得少了点什么,所以再这仍然将其列举出来。单向链表单向链表是链表中的一种,它的特点是只有一个指向下一个节点的指针域,对单向链表的访问需要从头部开始,根据指针域依次访问下一个节点,单向链表的结构如下图所示单向链表的创建单向链表的结构只需要一个数据域与指针域,这个数据域可以是一个结构体,也可以是多个基本数据类型;指针域是一个指向节点类型的指针,简单的定义如下:typedef struct _LIST_NODE { int nVal; struct _LIST_NODE *pNext; }LIST_NODE, *LPLIST_NODE;创建链表可以采用头插法或者尾插法来初始化一个有多个节点的链表头插法的示意图如下:它的过程就像示意图中展现的,首先使用新节点p的next指针指向当前的头节点把新节点加入到链表头,然后变更链表头指针,这样就在头部插入了一个节点,用代码来展示就是p->next = head; head = p;我们使用一个函数来封装就是LPLIST_NODE CreateListHead() { LPLIST_NODE pHead = NULL; while (TRUE) { LPLIST_NODE p = (LPLIST_NODE)malloc(sizeof(LIST_NODE)); if (NULL == p) { break; } memset(p, 0x00, sizeof(LIST_NODE)); printf("请输入节点值(为0时将退出创建节点):"); scanf_s("%d", &p->nVal); //这里不需要对链表为空单独讨论 //当链表为空时pHead 的值为NULL, 这两句代码就变为 //p->pNext = NULL; //pHead = p; p->pNext = pHead; pHead = p; if (p->nVal == 0) { break; } } return pHead; }采用尾插法的话,首先得获得链表的尾部 pTail, 然后使尾节点的next指针指向新节点,然后更新尾节点,用代码来表示就是pTail->next = p; pTail = p;下面的函数是采用尾插法来构建链表的例子//这个函数多定义了一个变量用来保存 // 可以不需要这个变量,这样在插入之前需要遍历一遍链表,以便找到尾节点 // 但是每次插入之前都需要遍历一遍,没有定义一个变量保存尾节点这种方式来的高效 LPLIST_NODE CreateListTail() { LPLIST_NODE pHead = NULL; LPLIST_NODE pTail = pHead; while (NULL != pTail && NULL != pTail->pNext) { pTail = pTail->pNext; } while (TRUE) { LPLIST_NODE p = (LPLIST_NODE)malloc(sizeof(LIST_NODE)); if (NULL == p) { break; } memset(p, 0x00, sizeof(LIST_NODE)); printf("请输入节点值(为0时将退出创建节点):"); scanf_s("%d", &p->nVal); //由于这种方法需要对尾节点的next域赋值,所以需要考虑链表为空的情况 if (NULL == pTail) { pHead = p; pTail = pHead; }else { pTail->pNext = p; pTail = p; } if (p->nVal == 0) { break; } } return pHead; }链表的遍历链表的每个节点在内存中不是连续的,所以它不能像数组那样根据下标来访问(当然可以利用C++中的运算符重载来实现使用下标访问),链表中的每一个节点都保存了下一个节点的地址,所以我们根据每个节点指向的下一个节点来依次访问每个节点,访问的代码如下:void TraverseList(LPLIST_NODE pHead) { while (NULL != pHead) { printf("%d\n", pHead->nVal); pHead = pHead->pNext; } }链表的删除链表的每个节点都是在堆上分配的,在不再使用的时候需要手工清除每个节点。清除时需要使用遍历的方法,一个个的删除,只是需要在遍历的指针移动到下一个节点前保存当前节点,以便能够删除当前节点,删除的函数如下void DestroyList(LPLIST_NODE pHead) { LPLIST_NODE pTmp = pHead; while (NULL != pTmp) { pTmp = pHead->pNext; delete pHead; pHead = pTmp; } }删除单个节点如上图所示,假设我们要删除q节点,那么首先需要遍历找到q的上一个节点p,将p的next指针指向q的下一个节点,也就是赋值为q的next指针的值,用代码表示就是p->next = q->next;删除节点的函数如下:void DeleteNode(LPLIST_NODE* ppHead, int nValue) { if (NULL == ppHead || NULL == *ppHead) { return; } LPLIST_NODE p, q; p = *ppHead; while (NULL != p) { if (nValue == p->nVal) { if (*ppHead == p) { *ppHead = p->pNext; free(p); }else { q->pNext = p->pNext; free(p); } p = NULL; q = NULL; break; } q = p; p = p->pNext; } }在上述代码中首先来遍历链表,找到要删除的节点p和它的上一个节点q,由于头节点没有上一个节点,所以需要特别判断一下需要删除的是否为头节点,如果为头结点,则直接将头指针指向它的下一个节点,然后删除头结点即可,如果不是则采用之前的方法来删除。任意位置插入节点如上图所示,如果需要在q节点之后插入p节点的话,需要两步,将q的next节点指向q,然后将q指向之前p的下一个节点,这个时候需要注意一下顺序,如果我们先执行q->next = p 的话,那么之前q的下一个节点的地址就被覆盖掉了,这个时候后面的节点都丢掉了,所以这里我们要先执行p->next = q->next 这条语句,然后在执行q->next = p下面是一个创建有序链表的例子,这个例子演示了在任意位置插入节点LPLIST_NODE CreateSortedList() { LPLIST_NODE pHead = NULL; while (TRUE) { LPLIST_NODE p = (LPLIST_NODE)malloc(sizeof(LIST_NODE)); if (NULL == p) { break; } memset(p, 0x00, sizeof(LIST_NODE)); printf("请输入节点值(为0时将退出创建节点):"); scanf_s("%d", &p->nVal); if (NULL == pHead) { pHead = p; }else { if (pHead->nVal > p->nVal) { p->pNext = pHead; pHead = p; }else { LPLIST_NODE q = pHead; LPLIST_NODE r = q; q = q->pNext; while (NULL != q && q->nVal < p->nVal) { r = q; q = q->pNext; } p->pNext = r->pNext; r->pNext = p; } } if (p->nVal == 0) { break; } } return pHead; }当确定新节点的值之后,首先遍历链表,直到找到比新节点中数值大的节点,那么这个新节点就是需要插入到该节点之前。在遍历的时候使用r来保存之前的节点。这里需要注意这些情况:链表为空:这种情况下,直接让头指针指向当前节点如果头节点本身就是大于新节点的值,这种情况下采用头插法,将新节点插入到头部如果链表中未找到比新节点的值更大的值,这种情况下直接采用尾插发在链表中找到比新节点值更大的节点,这种情况下,在链表中插入但是在代码中并没有考虑到尾部插入的情况,由于在尾部插入时,r等于尾节点,r->pNext 的值为NULL, 所以 p->pNext = r->pNext;r->pNext = p; 可以看成 p->pNext = NULL; r->pNext = p; 也就是将p的next指针指向空,让其作为尾节点,将之前的尾节点的next指针指向新节点。循环链表循环链表是建立在单向链表的基础之上的,循环链表的尾节点并不指向空,而是指向其他的节点,可以是头结点,可以是自身,也可以是链表中的其他节点,为了方便操作,一般将循环链表的尾节点的next指针指向头节点,它的操作与单链表的操作类似,只需要将之前判断尾节点的条件变为 pTail->pNext == pHead 即可。这里就不再详细分析每种操作了,直接给出代码LPLIST_NODE CreateLoopList() { LPLIST_NODE pHead = NULL; LPLIST_NODE pTail = pHead; while(1) { LPLIST_NODE p = (LPLIST_NODE)malloc(sizeof(LIST_NODE)); if (NULL == p) { break; } memset(p, 0x00, sizeof(LIST_NODE)); printf("请输入一个值:"); scanf_s("%d", &p->nVal); if (NULL == pHead) { pHead = p; p->pNext = pHead; pTail = pHead; }else { pTail->pNext = p; p->pNext = pHead; pTail = p; } if (0 == p->nVal) { break; } } return pHead; } void TraverseLoopList(LPLIST_NODE pHead) { LPLIST_NODE pTmp = pHead; if (NULL == pTmp) { return; } do { printf("%d, ", pTmp->nVal); pTmp = pTmp->pNext; } while (pTmp != pHead); } void DestroyLoopList(LPLIST_NODE pHead) { LPLIST_NODE pTmp = pHead; LPLIST_NODE pDestroy = pTmp; if (NULL == pTmp) { return; } do { pTmp = pDestroy->pNext; free(pDestroy); pDestroy = pTmp; }while (pHead != pTmp); }判断链表是否为循环链表在上面说过,循环链表的尾指针不一定指向头节点,它可以指向任何节点,那么该怎么判断一个节点是否为循环链表呢?既然它可以指向任意的节点,那么肯定是找不到尾节点的,而且堆内存的分配是随机的,我们也不可能按照指针变量的大小来判断哪个节点在前哪个在后。回想一下在学校跑一千米的时候是不是回出现这样的情况,跑的块的会领先跑的慢的一周?根据这种情形我们可以考虑使用这样一种办法:定义两个指针,一个一次走两步也是就是p = p->next->next, 一个慢指针一次走一步,也就是q = q->next,如果是循环链表,那么快指针在某个时候一定会领先慢指针一周,也就是达到 p == q 这个条件,否则就是非循环链表。根据这个思路,可以考虑写下如下代码:bool IsLoopList(LPLIST_NODE pHead) { if (NULL == pHead) { return false; } LPLIST_NODE p = pHead; LPLIST_NODE q = pHead->pNext; while (NULL != p && NULL != q && NULL != q->pNext && p != q) { p = p->pNext; q = q->pNext->pNext; } if (q == NULL || NULL == p || NULL == q->pNext) { return false; } return true; }双向链表之前在插入或者删除的时候,需要定义两个指针变量,让其中一个一直更在另一个的后面,单向链表有一个很大的问题,不能很方便的找到它的上一个节点,为了解决这一个问题,提出了双向链表,双向链表与单向相比,多了一个指针域,用来指向它的上一个节点,也就是如下图所示:双向链表的操作与单向链表的类似,只是多了一个指向前一个节点的指针域,它要考虑的情况与单向链表相似删除节点删除节点的示意图如下:假设删除的节点p,那么首先根据p的pre指针域,找到它的上一个节点q,采用与单向链表类似的操作:q->next = p->next; p->next->pre = q;下面是删除节点的例子:void DeleteDNode(LPDLIST_NODE* ppHead, int nValue) { if (NULL == ppHead || NULL == *ppHead) { return; } LPDLIST_NODE p = *ppHead; while (NULL != p && p->nVal != nValue) { p = p->pNext; } if (NULL == p) { return; } if (*ppHead == p) { *ppHead = (*ppHead)->pNext; p->pPre = NULL; free(p); } else if (p->pNext == NULL) { p->pPre->pNext = NULL; free(p); }else { p->pPre->pNext = p->pNext; p->pNext->pPre = p->pPre; } }插入节点插入节点的示意图如下:假设新节点为p,插入的位置为q,则插入操作可以进行如下操作p->next = q->next; p->pre = q; q->next->pre = p; q->next = p;也是一样要考虑不能覆盖q的next指针域否则可能存在找不到原来链表中q的下一个节点的情况。所以这里先对p的next指针域进行操作下面也是采用创建有序列表的例子LPDLIST_NODE CreateSortedDList() { LPDLIST_NODE pHead = NULL; while (1) { LPDLIST_NODE pNode = (LPDLIST_NODE)malloc(sizeof(DLIST_NODE)); if (NULL == pNode) { return pHead; } memset(pNode, 0x00, sizeof(DLIST_NODE)); printf("请输入一个整数:"); scanf_s("%d", &pNode->nVal); if(NULL == pHead) { pHead = pNode; }else { LPDLIST_NODE q = pHead; LPDLIST_NODE r = q; while (NULL != q && q->nVal < pNode->nVal) { r = q; q = q->pNext; } if (q == pHead) { pNode->pNext = pHead; pHead->pPre = pNode; pHead = pNode; }else if (NULL == q) { r->pNext = pNode; pNode->pPre = r; }else { pNode->pPre = r; pNode->pNext = q; r->pNext = pNode; q->pPre = pNode; } } LPDLIST_NODE q = pHead; LPDLIST_NODE r = q; if (0 == pNode->nVal) { break; } } return pHead; }链表还有一种是双向循环链表,对于这种链表主要是在双向链表的基础上,将头结点的pre指针指向某个节点,将尾节点的next节点指向某个节点,而且这两个指针可以指向同一个节点也可以指向不同的节点,一般在使用中都是head的pre节点指向尾节点,而tail的next节点指向头节点。这里就不再详细说明,这些链表只要掌握其中一种,剩下的很好掌握的。